bessely
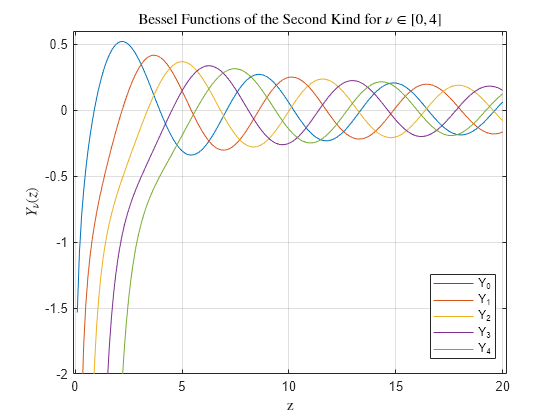
第二类贝塞尔函数
说明
示例
输入参数
详细信息
提示
贝塞尔函数与汉克尔函数相关,也称为第三类贝塞尔函数,
是 besselh,Jν(z) 是 besselj,Yν(z) 是 bessely。汉克尔函数同样构成贝塞尔方程的一组基本解(请参阅 besselh)。
参考
[1] Amos, D. E. “Algorithm 644: A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order.” ACM Transactions on Mathematical Software 12, no. 3 (September 1986): 265–273. https://dl.acm.org/doi/10.1145/7921.214331.
扩展功能
版本历史记录
在 R2006a 之前推出