kron

克罗内克张量积

语法

K = kron(A,B)

说明

K = kron(A,B) 返回矩阵 A 和 B 的克罗内克张量积。如果 A 是 m×n 矩阵，而 B 是 p×q 矩阵，则 kron(A,B) 是通过获取 A 元素与矩阵 B 元素之间的所有可能积而形成的一个 m*p×n*q 矩阵。

示例

全部折叠

分块对角矩阵

打开实时脚本

创建分块对角矩阵。

创建一个 4×4 单位矩阵以及一个要沿对角线重复的 2×2 矩阵。

A = eye(4);
B = [1 -1;-1 1];

使用 kron 计算克罗内克张量积。

K = kron(A,B)

K = 8×8

     1    -1     0     0     0     0     0     0
    -1     1     0     0     0     0     0     0
     0     0     1    -1     0     0     0     0
     0     0    -1     1     0     0     0     0
     0     0     0     0     1    -1     0     0
     0     0     0     0    -1     1     0     0
     0     0     0     0     0     0     1    -1
     0     0     0     0     0     0    -1     1

结果为一个 8×8 分块对角矩阵。

重复矩阵元素

打开实时脚本

通过重复元素来扩展矩阵大小。

创建一个 2×2 的全 1 矩阵，以及一个需要重复其元素的 2×3 矩阵。

A = [1 2 3; 4 5 6];
B = ones(2);

使用 kron 计算克罗内克张量积。

K = kron(A,B)

K = 4×6

     1     1     2     2     3     3
     1     1     2     2     3     3
     4     4     5     5     6     6
     4     4     5     5     6     6

结果为一个 4×6 分块矩阵。

稀疏拉普拉斯算子矩阵

打开实时脚本

此示例以可视方式呈现稀疏拉普拉斯算子矩阵。

离散拉普拉斯算子在二维 n×n 网格中的矩阵表示形式是 n*n×n*n 稀疏矩阵。每行或每列中最多有 5 个非零元素。可以采用一维差分算子的克罗内克积的形式生成矩阵。在此示例中，n = 5。

n = 5;
I = speye(n,n);
E = sparse(2:n,1:n-1,1,n,n);
D = E+E'-2*I;
A = kron(D,I)+kron(I,D);

使用 spy 以可视方式呈现稀疏模式。

spy(A,'k')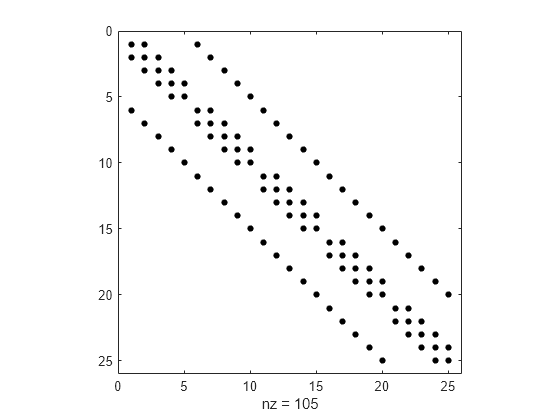

Figure contains an axes object. The axes object with xlabel nz = 105 contains a line object which displays its values using only markers.

输入参数

全部折叠

`A,B` — 输入矩阵
标量 | 向量 | 矩阵

输入矩阵，指定为标量、向量或矩阵。如果 A 或 B 是稀疏矩阵，则 kron 仅乘以非零元素，其结果也是稀疏矩阵。

详细信息

全部折叠

克罗内克张量积

如果 A 是 m×n 矩阵，而 B 是 p×q 矩阵，则 A 和 B 的克罗内克张量积是通过将 B 乘以 A 的各元素形成的一个大型矩阵。

$A \otimes B = [\begin{matrix} \begin{matrix} a_{11} B & a_{12} B \end{matrix} & \dots & a_{1 n} B \\ \begin{matrix} \begin{matrix} a_{21} B \\ ⋮ \end{matrix} & \begin{matrix} a_{22} B \\ ⋮ \end{matrix} \end{matrix} & \begin{matrix} \dots \\ ⋱ \end{matrix} & \begin{matrix} a_{2 n} B \\ ⋮ \end{matrix} \\ \begin{matrix} a_{m 1} B & a_{m 2} B \end{matrix} & \dots & a_{m n} B \end{matrix}] .$

例如，两个简单的 2×2 矩阵会生成

$\begin{array}{l} A = [\begin{matrix} 1 & - 2 \\ - 1 & 0 \end{matrix}], B = [\begin{matrix} 4 & - 3 \\ 2 & 3 \end{matrix}] \\ A \otimes B = [\begin{matrix} 1 \cdot 4 & 1 \cdot - 3 & - 2 \cdot 4 & - 2 \cdot - 3 \\ 1 \cdot 2 & 1 \cdot 3 & - 2 \cdot 2 & - 2 \cdot 3 \\ - 1 \cdot 4 & - 1 \cdot - 3 & 0 \cdot 4 & 0 \cdot - 3 \\ - 1 \cdot 2 & - 1 \cdot 3 & 0 \cdot 2 & 0 \cdot 3 \end{matrix}] = [\begin{matrix} 4 & - 3 & - 8 & 6 \\ 2 & 3 & - 4 & - 6 \\ - 4 & 3 & 0 & 0 \\ - 2 & - 3 & 0 & 0 \end{matrix}] . \end{array}$

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

kron 函数完全支持 GPU 数组。要在 GPU 上运行该函数，请将输入数据指定为 gpuArray (Parallel Computing Toolbox)。有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

此函数完全支持分布式数组。有关详细信息，请参阅使用分布式数组运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

另请参阅

tensorprod | hankel | toeplitz | dot | cross

kron

语法

说明

示例

分块对角矩阵

重复矩阵元素

稀疏拉普拉斯算子矩阵

输入参数

A,B — 输入矩阵 标量 | 向量 | 矩阵

详细信息

克罗内克张量积

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成 使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组 使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

版本历史记录

另请参阅

`A,B` — 输入矩阵
标量 | 向量 | 矩阵

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。