Main Content

merton

Merton jump diffusion model

Since R2020a

expand all in page

Description

Creates and displays a merton object, which derives from the gbm object.

The merton model, based on the Merton76 model, allows you to simulate sample paths of NVars state variables driven by NBrowns Brownian motion sources of risk and NJumps compound Poisson processes representing the arrivals of important events over NPeriods consecutive observation periods. The simulation approximates continuous-time merton stochastic processes.

You can simulate any vector-valued merton process of the form

dXt=B(t,Xt)Xtdt+D(t,Xt)V(t,xt)dWt+Y(t,Xt,Nt)XtdNt

Here:

  • Xt is an NVars-by-1 state vector of process variables.

  • B(t,Xt) is an NVars-by-NVars matrix of generalized expected instantaneous rates of return.

  • D(t,Xt) is an NVars-by-NVars diagonal matrix in which each element along the main diagonal is the corresponding element of the state vector.

  • V(t,Xt) is an NVars-by-NVars matrix of instantaneous volatility rates.

  • dWt is an NBrowns-by-1 Brownian motion vector.

  • Y(t,Xt,Nt) is an NVars-by-NJumps matrix-valued jump size function.

  • dNt is an NJumps-by-1 counting process vector.

Creation

Syntax

Merton = merton(Return,Sigma,JumpFreq,JumpMean,JumpVol)
Merton = merton(___,Name,Value)

Description

Merton = merton(Return,Sigma,JumpFreq,JumpMean,JumpVol) creates a default merton object. Specify the required inputs as one of two types:

  • MATLAB® array. Specify an array to indicate a static (non-time-varying) parametric specification. This array fully captures all implementation details, which are clearly associated with a parametric form.

  • MATLAB function. Specify a function to provide indirect support for virtually any static, dynamic, linear, or nonlinear model. This parameter is supported by an interface because all implementation details are hidden and fully encapsulated by the function.

Note

You can specify combinations of array and function input parameters as needed. Moreover, a parameter is identified as a deterministic function of time if the function accepts a scalar time t as its only input argument. Otherwise, a parameter is assumed to be a function of time t and state Xt and is invoked with both input arguments.

example

Merton = merton(___,Name,Value) sets Properties using name-value pair arguments in addition to the input arguments in the preceding syntax. Enclose each property name in quotes.

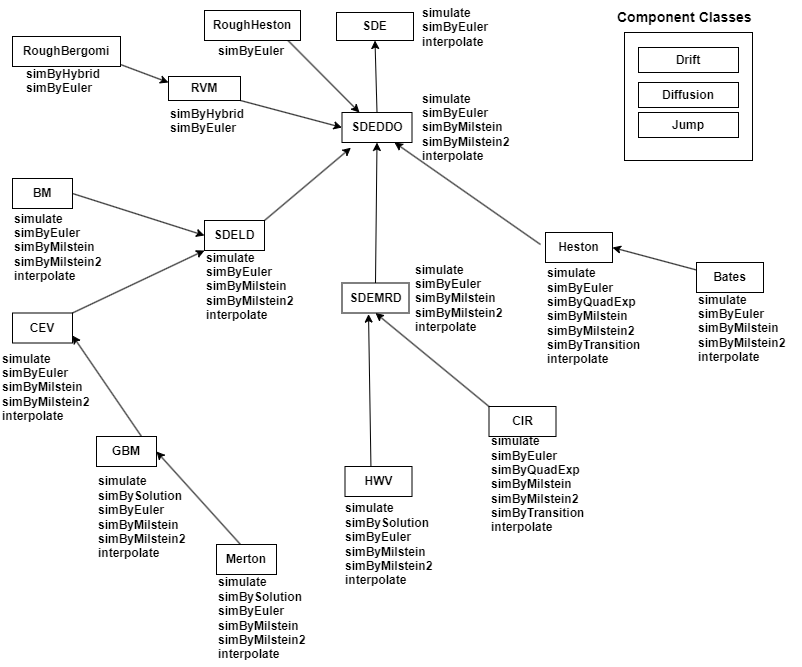
The merton object has the following Properties:

  • StartTime — Initial observation time

  • StartState — Initial state at time StartTime

  • Correlation — Access function for the Correlation input argument

  • Drift — Composite drift-rate function

  • Diffusion — Composite diffusion-rate function

  • Simulation — A simulation function or method

example

Input Arguments

expand all

Expected mean instantaneous rates of asset return, denoted as B(t,Xt), specified as an array, a deterministic function of time, or a deterministic function of time and state.

If you specify Return as an array, it must be an NVars-by-NVars matrix representing the expected (mean) instantaneous rate of return.

If you specify Return as a deterministic function of time, when you call Return with a real-valued scalar time t as its only input, it must return an NVars-by-NVars matrix.

If you specify Return as a deterministic function of time and state, it must return an NVars-by-NVars matrix when you call it with two inputs:

  • A real-valued scalar observation time t

  • An NVars-by-1 state vector Xt

Data Types: double | function_handle

Instantaneous volatility rates, denoted as V(t,Xt), specified as an array, a deterministic function of time, or a deterministic function of time and state.

If you specify Sigma as an array, it must be an NVars-by-NBrowns matrix of instantaneous volatility rates or a deterministic function of time. In this case, each row of Sigma corresponds to a particular state variable. Each column corresponds to a particular Brownian source of uncertainty, and associates the magnitude of the exposure of state variables with sources of uncertainty.

If you specify Sigma as a deterministic function of time, when you call Sigma with a real-valued scalar time t as its only input, it must return an NVars-by-NBrowns matrix.

If you specify Sigma as a deterministic function of time and state, it must return an NVars-by-NBrowns matrix when you call it with two inputs:

  • A real-valued scalar observation time t

  • An NVars-by-1 state vector Xt

Note

Although merton enforces no restrictions for Sigma, volatilities are usually nonnegative.

Data Types: double | function_handle

Instantaneous jump frequencies representing the intensities (the mean number of jumps per unit time) of the Poisson processes Nt that drive the jump simulation, specified as an array, a deterministic function of time, or a deterministic function of time and state.

If you specify JumpFreq as an array, it must be an NJumps-by-1 vector.

If you specify JumpFreq as a deterministic function of time, when you call JumpFreq with a real-valued scalar time t as its only input, JumpFreq must produce an NJumps-by-1 vector.

If you specify JumpFreq as a deterministic function of time and state, it must return an NVars-by-NBrowns matrix when you call it with two inputs:

  • A real-valued scalar observation time t

  • An NVars-by-1 state vector Xt

Data Types: double | function_handle

Instantaneous mean of random percentage jump sizes J, where log(1+J) is normally distributed with mean (log(1+JumpMean) - 0.5 × JumpVol2) and standard deviation JumpVol, specified as decimal using an array, a deterministic function of time, or a deterministic function of time and state. For instance, an expected jump effect of 20% on the price of an underlying asset must be input as 0.2 instead of 20.

If you specify JumpMean as an array, it must be an NVars-by-NJumps matrix.

If you specify JumpMean as a deterministic function of time, when you cal JumpMean with a real-valued scalar time t as its only input, it must return an NVars-by-NJumps matrix.

If you specify JumpMean as a deterministic function of time and state, it must return an NVars-by-NJumps matrix when you call it with two inputs:

  • A real-valued scalar observation time t

  • An NVars-by-1 state vector Xt

Data Types: double | function_handle

Instantaneous standard deviation of log(1+J), specified as an array, a deterministic function of time, or a deterministic function of time and state.

If you specify JumpVol as an array, it must be an NVars-by-NJumps matrix.

If you specify JumpVol as a deterministic function of time, when you call JumpVol with a real-valued scalar time t as its only input, it must return an NVars-by-NJumps matrix.

If you specify JumpVol as a deterministic function of time and state, it must return an NVars-by-NJumps matrix when you call it with two inputs:

  • A real-valued scalar observation time t

  • An NVars-by-1 state vector Xt

Data Types: double | function_handle

Properties

expand all

Starting time of first observation, applied to all state variables, specified as a scalar.

Data Types: double

Initial values of state variables, specified as a scalar, column vector, or matrix.

If StartState is a scalar, merton applies the same initial value to all state variables on all trials.

If StartState is a column vector, merton applies a unique initial value to each state variable on all trials.

If StartState is a matrix, merton applies a unique initial value to each state variable on each trial.

Data Types: double

Correlation between Gaussian random variates drawn to generate the Brownian motion vector (Wiener processes), specified as an NBrowns-by-NBrowns positive semidefinite matrix, or as a deterministic function Ct that accepts the current time t and returns an NBrowns-by-NBrowns positive semidefinite correlation matrix. If Correlation is not a symmetric positive semidefinite matrix, use nearcorr to create a positive semidefinite matrix for a correlation matrix.

A Correlation matrix represents a static condition.

If you specify Correlation as a deterministic function of time, you can specify a dynamic correlation structure.

Data Types: double

This property is read-only.

Drift-rate component of continuous-time stochastic differential equations (SDEs), specified as a drift object or function accessible by (t, Xt).

The drift-rate specification supports the simulation of sample paths of NVars state variables driven by NBrowns Brownian motion sources of risk over NPeriods consecutive observation periods, approximating continuous-time stochastic processes.

Use the drift function to create drift objects of the form

F(t,Xt)=A(t)+B(t)Xt

Here:

  • A is an NVars-by-1 vector-valued function accessible using the (t, Xt) interface.

  • B is an NVars-by-NVars matrix-valued function accessible using the (t, Xt) interface.

The displayed parameters for a drift object are:

  • Rate — Drift-rate function, F(t,Xt)

  • A — Intercept term, A(t,Xt), of F(t,Xt)

  • B — First-order term, B(t,Xt), of F(t,Xt)

A and B enable you to query the original inputs. The function stored in Rate fully encapsulates the combined effect of A and B.

Specifying AB as MATLAB double arrays clearly associates them with a linear drift rate parametric form. However, specifying either A or B as a function allows you to customize virtually any drift-rate specification.

Note

You can express drift and diffusion objects in the most general form to emphasize the functional (t, Xt) interface. However, you can specify the components A and B as functions that adhere to the common (t, Xt) interface, or as MATLAB arrays of appropriate dimension.

Example: F = drift(0, 0.1) % Drift-rate function F(t,X)

Data Types: object

This property is read-only.

Diffusion-rate component of continuous-time stochastic differential equations (SDEs), specified as a drift object or function accessible by (t, Xt).

The diffusion-rate specification supports the simulation of sample paths of NVars state variables driven by NBrowns Brownian motion sources of risk over NPeriods consecutive observation periods for approximating continuous-time stochastic processes.

Use the diffusion function to create diffusion objects of the form

G(t,Xt)=D(t,Xtα(t))V(t)

Here:

  • D is an NVars-by-NVars diagonal matrix-valued function.

  • Each diagonal element of D is the corresponding element of the state vector raised to the corresponding element of an exponent Alpha, which is an NVars-by-1 vector-valued function.

  • V is an NVars-by-NBrowns matrix-valued volatility rate function Sigma.

  • Alpha and Sigma are also accessible using the (t, Xt) interface.

The displayed parameters for a diffusion object are:

  • Rate — Diffusion-rate function, G(t,Xt)

  • Alpha — State vector exponent, which determines the format of D(t,Xt) of G(t,Xt)

  • Sigma — Volatility rate, V(t,Xt), of G(t,Xt)

Alpha and Sigma enable you to query the original inputs. (The combined effect of the individual Alpha and Sigma parameters is fully encapsulated by the function stored in Rate.) The Rate functions are the calculation engines for the drift and diffusion objects, and are the only parameters required for simulation.

Note

You can express drift and diffusion objects in the most general form to emphasize the functional (t, Xt) interface. However, you can specify the components A and B as functions that adhere to the common (t, Xt) interface, or as MATLAB arrays of appropriate dimension.

Example: G = diffusion(1, 0.3) % Diffusion-rate function G(t,X)

Data Types: object

User-defined simulation function or SDE simulation method, specified as a function or SDE simulation method.

Data Types: function_handle

Object Functions

simByEulerSimulate Merton jump diffusion sample paths by Euler approximation
simBySolutionSimulate approximate solution of diagonal-drift Merton jump diffusion process
simByMilsteinSimulate diagonal diffusion Merton sample paths by Milstein approximation
simByMilstein2Simulate diagonal diffusion Merton sample paths by second order Milstein approximation
simulateSimulate multivariate stochastic differential equations (SDEs) for SDE, BM, GBM, CEV, CIR, HWV, Heston, SDEDDO, SDELD, SDEMRD, Merton, or Bates models

Examples

collapse all

Open Live Script

Merton jump diffusion models allow you to simulate sample paths of NVARS state variables driven by NBROWNS Brownian motion sources of risk and NJumps compound Poisson processes representing the arrivals of important events over NPeriods consecutive observation periods. The simulation approximates continuous-time merton stochastic processes.

Create a merton object. 

AssetPrice = 80;
            Return = 0.03;
            Sigma = 0.16;
            JumpMean = 0.02;
            JumpVol = 0.08;
            JumpFreq = 2;
            
            mertonObj = merton(Return,Sigma,JumpFreq,JumpMean,JumpVol,...
                'startstat',AssetPrice)
mertonObj = 
   Class MERTON: Merton Jump Diffusion
   ----------------------------------------
     Dimensions: State = 1, Brownian = 1
   ----------------------------------------
      StartTime: 0
     StartState: 80
    Correlation: 1
          Drift: drift rate function F(t,X(t)) 
      Diffusion: diffusion rate function G(t,X(t)) 
     Simulation: simulation method/function simByEuler
          Sigma: 0.16
         Return: 0.03
       JumpFreq: 2
       JumpMean: 0.02
        JumpVol: 0.08

More About

expand all

Algorithms

The Merton jump diffusion model (Merton 1976) is an extension of the Black-Scholes model, and models sudden asset price movements (both up and down) by adding the jump diffusion parameters with the Poisson process Pt.

Under the risk-neutral measure the model is expressed as follows

dSt=(γ−q−λpμj)Stdt+σMStdWt+JStdPtprob(dPt=1)=λpdt

Here:

ᵞ is the continuous risk-free rate.

q is the continuous dividend yield.

J is the random percentage jump size conditional on the jump occurring, where

ln(1+J)~N(ln(1+uj)−δ22,δ2

(1+J) has a lognormal distribution:

1(1+J)δ2πexp{−[ln(1+J)−(ln(1+μj)−δ22]22δ2}

Here:

μj is the mean of J(μj > -1).

ƛp is the annual frequency (intensity) of the Poisson process Pt (ƛp ≥ 0).

σM is the volatility of the asset price (σM> 0).

Under this formulation, extreme events are explicitly included in the stochastic differential equation as randomly occurring discontinuous jumps in the diffusion trajectory. Therefore, the disparity between observed tail behavior of log returns and that of Brownian motion is mitigated by the inclusion of a jump mechanism.

References

[1] Aït-Sahalia, Yacine. “Testing Continuous-Time Models of the Spot Interest Rate.” Review of Financial Studies 9, no. 2 ( Apr. 1996): 385–426.

[2] Aït-Sahalia, Yacine. “Transition Densities for Interest Rate and Other Nonlinear Diffusions.” The Journal of Finance 54, no. 4 (Aug. 1999): 1361–95.

[3] Glasserman, Paul. Monte Carlo Methods in Financial Engineering. New York: Springer-Verlag, 2004.

[4] Hull, John C. Options, Futures and Other Derivatives. 7th ed, Prentice Hall, 2009.

[5] Johnson, Norman Lloyd, Samuel Kotz, and Narayanaswamy Balakrishnan. Continuous Univariate Distributions. 2nd ed. Wiley Series in Probability and Mathematical Statistics. New York: Wiley, 1995.

[6] Shreve, Steven E. Stochastic Calculus for Finance. New York: Springer-Verlag, 2004.

Version History

Introduced in R2020a

expand all

See Also

| | |

Topics