sdeld
采用线性漂移 (SDELD) 模型的 SDE
说明
创建并显示一个 SDE 对象,该对象的漂移率以线性漂移率形式表示,并且该对象派生自 sdeddo 类(来自漂移和扩散对象的 SDE)。
使用 sdeld 对象模拟 NVars 个状态变量(以线性漂移率形式表示)的样本路径。这些对象为均值回归漂移率提供一个参数化替代(请参阅 sdemrd)。
这些状态变量在 NPeriods 个连续观测周期内由 NBrowns 个布朗运动风险源驱动,用线性漂移率函数逼近连续时间随机过程。
使用 sdeld 对象可模拟以下形式的任意向量值 SDELD:
,其中:
Xt 是过程变量的
NVars×1状态向量。A 是一个
NVars×1向量。B 是一个
NVars×NVars矩阵。D 是
NVars×NVars对角矩阵,其中沿着主对角线的每个元素是状态向量对应元素的 α 指数次幂。V 是
NVars×NBrowns瞬时波动率矩阵。dWt 是
NBrowns×1布朗运动向量。
创建对象
描述
SDELD = sdeld(___,Name,Value)Name,Value 对组参量指定的其他选项创建一个 SDELD 对象。
Name 是属性名称,Value 是其对应的值。Name 必须放在单引号 ('') 内。您可以按任意顺序指定多个名称-值对组参量,如 Name1,Value1,…,NameN,ValueN。
SDELD 对象具有下面显示的属性:
StartTime- 初始观测时间StartState-StartTime时的初始状态Correlation-Correlation输入参量的访问函数,可作为时间的函数进行调用Drift- 复合漂移率函数,可作为时间和状态的函数进行调用Diffusion- 复合扩散率函数,可作为时间和状态的函数进行调用A-A输入参量的访问函数,可作为时间和状态的函数进行调用B-B输入参量的访问函数,可作为时间和状态的函数进行调用Alpha-Alpha输入参量的访问函数,可作为时间和状态的函数进行调用Sigma-Sigma输入参量的访问函数,可作为时间和状态的函数进行调用Simulation- 模拟函数或方法
输入参量
输出参量
属性
对象函数
interpolate | Brownian interpolation of stochastic differential equations (SDEs) for
SDE, BM, GBM,
CEV, CIR, HWV,
Heston, SDEDDO, SDELD, or
SDEMRD models |
simulate | Simulate multivariate stochastic differential equations (SDEs) for
SDE, BM, GBM,
CEV, CIR, HWV,
Heston, SDEDDO, SDELD,
SDEMRD, Merton, or Bates
models |
simByEuler | Euler simulation of stochastic differential equations (SDEs) for
SDE, BM, GBM,
CEV, CIR, HWV,
Heston, SDEDDO, SDELD, or
SDEMRD models |
simByMilstein | Simulate diagonal diffusion for BM, GBM,
CEV, HWV, SDEDDO,
SDELD, or SDEMRD sample paths by Milstein
approximation |
simByMilstein2 | Simulate BM, GBM, CEV,
HWV, SDEDDO, SDELD,
SDEMRD process sample paths by second order Milstein
approximation |
示例
详细信息
算法
当您将必需的输入参数指定为数组时,它们将与特定的参数化形式相关联。相比之下,当您将任一必需的输入参数指定为函数时,几乎可以自定义任何设定。
在没有输入的情况下访问输出参数只会返回原始输入设定。因此,当您不带输入调用这些参数时,它们的行为就像简单的属性,您可以测试指定的原始输入的数据类型(是双精度值还是函数,即是静态的还是动态的)。这对于验证和设计方法非常有用。
当您使用输入调用这些参数时,它们的行为类似于函数,给人以动态行为的印象。该参数接受观测时间 t 和状态向量 Xt,并返回适当维度的数组。即使您最初将输入指定为数组,sdeld 也会将其视为时间和状态的静态函数,这样可以确保所有参数都可由同一接口访问。
参考
[1] Aït-Sahalia, Yacine. “Testing Continuous-Time Models of the Spot Interest Rate.” Review of Financial Studies, vol. 9, no. 2, Apr. 1996, pp. 385–426.
[2] Aït-Sahalia, Yacine. “Transition Densities for Interest Rate and Other Nonlinear Diffusions.” The Journal of Finance, vol. 54, no. 4, Aug. 1999, pp. 1361–95.
[3] Glasserman, Paul. Monte Carlo Methods in Financial Engineering. Springer, 2004.
[4] Hull, John. Options, Futures and Other Derivatives. 7th ed, Prentice Hall, 2009.
[5] Johnson, Norman Lloyd, et al. Continuous Univariate Distributions. 2nd ed, Wiley, 1994.
[6] Shreve, Steven E. Stochastic Calculus for Finance. Springer, 2004.
版本历史记录
在 R2008a 中推出另请参阅
drift | diffusion | sdeddo | simByEuler | nearcorr
主题
- 线性漂移模型
- 实现多维股票市场模型,实现 3:使用 SDELD、CEV 和 GBM 对象
- Simulating Equity Prices
- Simulating Interest Rates
- Stratified Sampling
- Price American Basket Options Using Standard Monte Carlo and Quasi-Monte Carlo Simulation
- 基础 SDE 模型
- 漂移和扩散模型
- 线性漂移模型
- Parametric Models
- SDEs
- SDE Models
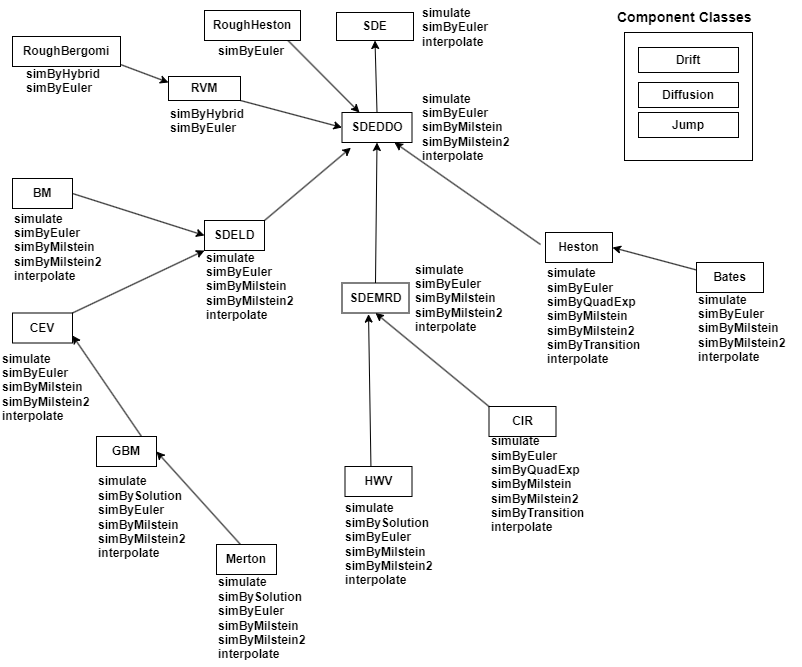
- SDE Class Hierarchy
- 准蒙特卡罗模拟
- Performance Considerations