sdeddo

基于漂移和扩散分量建立随机微分方程 (SDEDDO) 模型

全页展开

说明

创建和显示 sdeddo 对象，该对象使用 drift 和 diffusion 类的对象进行了实例化。受限 sdeddo 对象包含 drift 和 diffusion 输入对象；因此，您可以直接访问它们显示的参数。

这种抽象也将漂移率和扩散率对象的概念概括为 sdeddo 针对时间 t 和状态 Xt 的特定值计算的函数。与 sde 对象一样，使用 sdeddo 对象可以模拟 NVars 个状态变量（由 NBrowns 个布朗运动风险源驱动）在 NPeriods 个连续观测周期内的样本路径，以便逼近连续时间随机过程。

使用此方法可以模拟以下形式的任意向量值 SDEDDO：

dXt=F(t,Xt)dt+G(t,Xt)dWt(1)
，其中：

  • Xt 是过程变量的 NVars×1 状态向量。

  • dWt 是 NBrowns×1 布朗运动向量。

  • F 是一个 NVars×1 向量值漂移率函数。

  • G 是一个 NVars×NBrowns 矩阵值扩散率函数。

创建对象

语法

SDEDDO = sdeddo(DriftRate,DiffusionRate)
SDEDDO = sdeddo(___,Name,Value)

描述

SDEDDO = sdeddo(DriftRate,DiffusionRate) 创建一个默认的 SDEDDO 对象。

示例

SDEDDO = sdeddo(___,Name,Value) 使用由一个或多个 Name,Value 对组参量指定的其他选项创建一个 SDEDDO 对象。

Name 是属性名称，Value 是其对应的值。Name 必须放在单引号 ('') 内。您可以按任意顺序指定多个名称-值对组参量，如 Name1,Value1,…,NameN,ValueN。

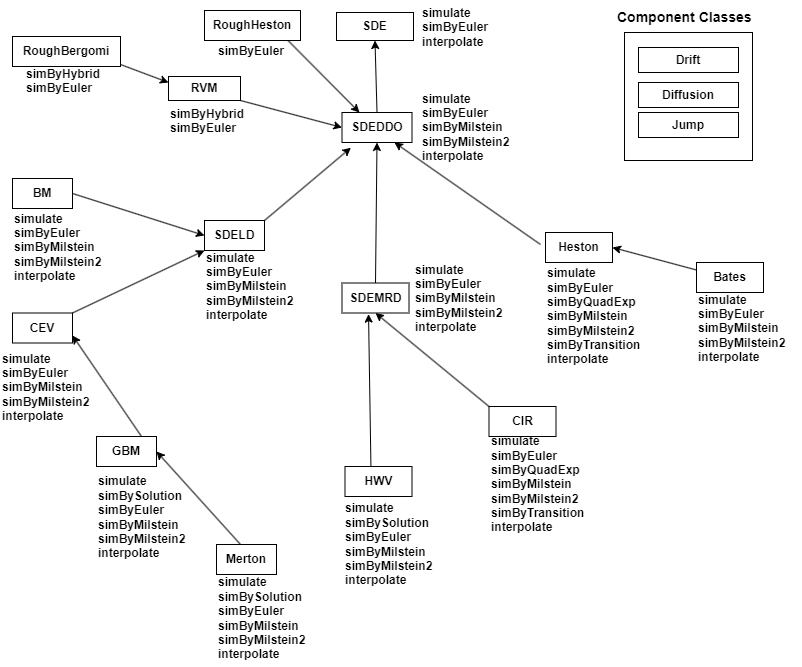
SDEDDO 对象具有下面显示的属性：

  • StartTime - 初始观测时间

  • StartState - StartTime 时的初始状态

  • Correlation - Correlation 输入参量的访问函数，可作为时间的函数进行调用

  • Drift - 复合漂移率函数，可作为时间和状态的函数进行调用

  • Diffusion - 复合扩散率函数，可作为时间和状态的函数进行调用

  • A - A 漂移率属性的访问函数，可作为时间和状态的函数进行调用

  • B - B 漂移率属性的访问函数，可作为时间和状态的函数进行调用

  • Alpha - Alpha 扩散率属性的访问函数，可作为时间和状态的函数进行调用

  • Sigma - Sigma 扩散率属性的访问函数，可作为时间和状态的函数进行调用

  • Simulation - 模拟函数或方法

示例

输入参量

全部展开

DriftRate 是用户定义的漂移率函数，表示参数 F，指定为向量或 drift 类的对象。

DriftRate 是一个函数，在使用下面两个输入调用时返回一个 NVars×1 漂移率向量：

  • 实值标量观测时间 t。

  • NVars×1 状态向量 Xt。

或者，DriftRate 也可以是一个 drift 类的对象，其中封装有漂移率设定。不过，在这种情况下，sde 仅使用对象的 Rate 参数。有关 drift 对象的详细信息，请参阅 drift。

数据类型: double

DiffusionRate 是用户定义的扩散率函数，表示参数 G，指定为矩阵或 diffusion 类的对象。

DiffusionRate 是一个函数，在使用下面两个输入调用时返回一个 NVars×NBrowns 扩散率矩阵：

  • 实值标量观测时间 t。

  • NVars×1 状态向量 Xt。

或者，DiffusionRate 也可以是一个 diffusion 类的对象，其中封装有扩散率设定。不过，在这种情况下，sde 仅使用对象的 Rate 参数。有关 diffusion 对象的详细信息，请参阅 diffusion。

数据类型: double

输出参量

全部展开

SDEDDO 模型，以 SDEDDO 对象形式返回。

属性

全部展开

首次观测的开始时间，应用于所有状态变量，指定为标量

数据类型: double

状态变量的初始值，指定为标量、列向量或矩阵。

如果 StartState 是一个标量，则 sdeddo 在所有试验中对所有状态变量应用相同的初始值。

如果 StartState 是一个列向量，则 sdeddo 在所有试验中对每个状态变量应用唯一的初始值。

如果 StartState 是一个矩阵，则 sdeddo 在每次试验中对每个状态变量应用唯一的初始值。

数据类型: double

为生成布朗运动向量（维纳过程）而抽取的高斯随机变量之间的相关性，指定为 NBrowns×NBrowns 半正定矩阵或确定性函数 C(t)，接受当前时间 t 并返回 NBrowns×NBrowns 半正定相关矩阵。如果 Correlation 不是对称半正定矩阵，则使用 nearcorr 为相关矩阵创建半正定矩阵。

Correlation 矩阵表示静态条件。

作为时间的确定性函数，Correlation 允许您指定动态相关结构体。

数据类型: double

用户自定义的模拟函数或 SDE 模拟方法，指定为函数或 SDE 模拟方法。

数据类型: function_handle

此 属性 为只读。

连续时间随机微分方程 (SDE) 的漂移率分量，指定为可由 (t, Xt) 访问的漂移对象或函数。

漂移率设定支持模拟 NVars 个状态变量（由 NBrowns 个布朗运动风险源驱动）在 NPeriods 个连续观测周期内的样本路径，逼近连续时间随机过程。

drift 类允许使用以下形式的 drift 创建漂移率对象：

F(t,Xt)=A(t)+B(t)Xt

其中：

  • A 是一个 NVars×1 向量值函数，可使用 (t, Xt) 接口访问。

  • B 是一个 NVars×NVars 矩阵值函数，可使用 (t, Xt) 接口访问。

drift 对象显示的参数是：

  • Rate:漂移率函数 F(t,Xt)

  • A:F(t,Xt) 的截断项 A(t,Xt)

  • B:F(t,Xt) 的一阶项 B(t,Xt)

A 和 B 让您可以查询原始输入。存储在 Rate 中的函数完全封装了 A 和 B 的组合效果。

当指定为 MATLAB® 双精度数组时，输入 A 和 B 显然与线性漂移率参数式相关联。然而，指定 A 或 B 为函数，几乎可以让您自定义任何漂移率设定。

注意

您可以采用最一般的形式来表达 drift 和 diffusion 类，以突出 (t, Xt) 函数式接口。不过，在指定分量 A 和 B 时，可以将其指定为支持通用 (t, Xt) 接口，也可以指定为具有适当维度的 MATLAB 数组。

示例: F = drift(0, 0.1) % Drift rate function F(t,X)

数据类型: struct | double

此 属性 为只读。

连续时间随机微分方程 (SDE) 的扩散率分量，指定为可由 (t, Xt) 访问的漂移对象或函数。

扩散率设定支持模拟 NVars 个状态变量（由 NBrowns 个布朗运动风险源驱动）在 NPeriods 个连续观测周期内的样本路径，逼近连续时间随机过程。

diffusion 类允许使用 diffusion 创建扩散率对象：

G(t,Xt)=D(t,Xtα(t))V(t)

其中：

  • D 是一个 NVars×NVars 对角矩阵值函数。

  • D 的每个对角元素是状态向量对应元素的 Alpha 指数次幂，该指数是一个 NVars×1 向量值函数。

  • V 是一个 NVars×NBrowns 矩阵值波动率函数 Sigma。

  • Alpha 和 Sigma 也可以使用 (t, Xt) 接口访问。

diffusion 对象显示的参数是：

  • Rate:扩散率函数 G(t,Xt)。

  • Alpha:状态向量指数，决定了 G(t,Xt) 的 D(t,Xt) 的格式。

  • Sigma:G(t,Xt) 的波动率 V(t,Xt)。

Alpha 和 Sigma 让您可以查询原始输入。（单个 Alpha 和 Sigma 参数由存储在 Rate 中的函数完全封装。）Rate 函数是 drift 和 diffusion 对象的计算引擎，而这一函数是模拟所需的唯一参数。

注意

您可以采用最一般的形式来表达 drift 和 diffusion 类，以突出 (t, Xt) 函数式接口。不过，在指定分量 A 和 B 时，可以将其指定为支持通用 (t, Xt) 接口，也可以指定为具有适当维度的 MATLAB 数组。

示例: G = diffusion(1, 0.3) % Diffusion rate function G(t,X)

数据类型: struct | double

对象函数

interpolateBrownian interpolation of stochastic differential equations (SDEs) for SDE, BM, GBM, CEV, CIR, HWV, Heston, SDEDDO, SDELD, or SDEMRD models
simulateSimulate multivariate stochastic differential equations (SDEs) for SDE, BM, GBM, CEV, CIR, HWV, Heston, SDEDDO, SDELD, SDEMRD, Merton, or Bates models
simByEulerEuler simulation of stochastic differential equations (SDEs) for SDE, BM, GBM, CEV, CIR, HWV, Heston, SDEDDO, SDELD, or SDEMRD models
simByMilsteinSimulate diagonal diffusion for BM, GBM, CEV, HWV, SDEDDO, SDELD, or SDEMRD sample paths by Milstein approximation
simByMilstein2Simulate BM, GBM, CEV, HWV, SDEDDO, SDELD, SDEMRD process sample paths by second order Milstein approximation

示例

全部折叠

打开实时脚本

sdeddo 类派生自基础 sde 类。若要使用此类，您必须将漂移率和扩散率对象传递给 sdeddo 函数。

创建 drift 和 diffusion 比率对象： 

F = drift(0, 0.1);      % Drift rate function F(t,X)
G = diffusion(1, 0.3);  % Diffusion rate function G(t,X)

将这些函数传递给 sdeddo 函数以创建 sdeddo 类的对象 obj： 

obj = sdeddo(F, G)      % dX = F(t,X)dt + G(t,X)dW
obj = 
   Class SDEDDO: SDE from Drift and Diffusion Objects
   --------------------------------------------------
     Dimensions: State = 1, Brownian = 1
   --------------------------------------------------
      StartTime: 0
     StartState: 1
    Correlation: 1
          Drift: drift rate function F(t,X(t)) 
      Diffusion: diffusion rate function G(t,X(t)) 
     Simulation: simulation method/function simByEuler
              A: 0
              B: 0.1
          Alpha: 1
          Sigma: 0.3

在此示例中，对象显示了与输入 drift 和 diffusion 对象相关联的额外参数。

详细信息

全部展开

算法

当您将必需的输入参数指定为数组时，它们将与特定的参数化形式相关联。相比之下，当您将任一必需的输入参数指定为函数时，几乎可以自定义任何设定。

在没有输入的情况下访问输出参数只会返回原始输入设定。因此，当您不带输入调用这些参数时，它们的行为就像简单的属性，您可以测试指定的原始输入的数据类型（是双精度值还是函数，即是静态的还是动态的）。这对于验证和设计方法非常有用。

当您使用输入调用这些参数时，它们的行为类似于函数，给人以动态行为的印象。该参数接受观测时间 t 和状态向量 Xt，并返回适当维度的数组。即使您最初将输入指定为数组，sdeddo 也会将其视为时间和状态的静态函数，这样可以确保所有参数都可由同一接口访问。

参考

[1] Aït-Sahalia, Yacine. “Testing Continuous-Time Models of the Spot Interest Rate.” Review of Financial Studies, vol. 9, no. 2, Apr. 1996, pp. 385–426.

[2] Aït-Sahalia, Yacine. “Transition Densities for Interest Rate and Other Nonlinear Diffusions.” The Journal of Finance, vol. 54, no. 4, Aug. 1999, pp. 1361–95.

[3] Glasserman, Paul. Monte Carlo Methods in Financial Engineering. Springer, 2004.

[4] Hull, John. Options, Futures and Other Derivatives. 7th ed, Prentice Hall, 2009.

[5] Johnson, Norman Lloyd, et al. Continuous Univariate Distributions. 2nd ed, Wiley, 1994.

[6] Shreve, Steven E. Stochastic Calculus for Finance. Springer, 2004.

版本历史记录

在 R2008a 中推出

全部展开

另请参阅

| | | | | |

主题