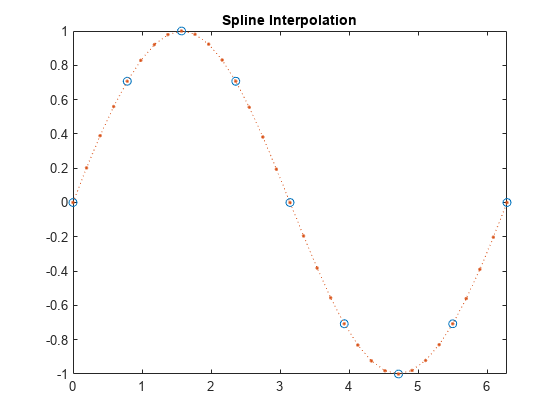
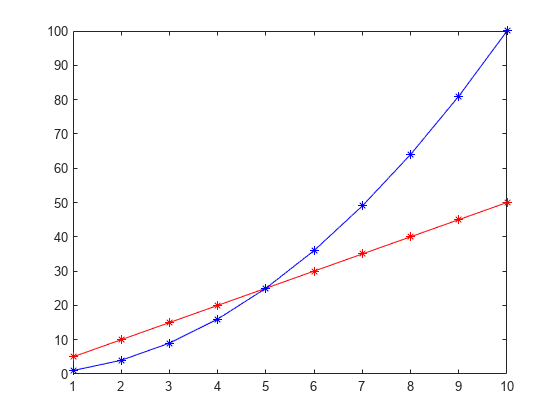
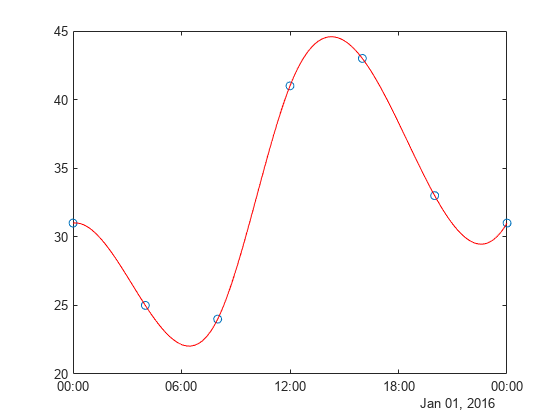
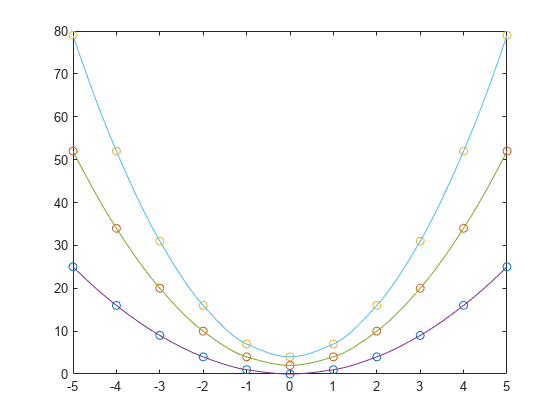
interp1

一维数据插值（表查找）

全页折叠

语法

vq = interp1(x,v,xq)

vq = interp1(x,v,xq,method)

vq = interp1(x,v,xq,method,extrapolation)

vq = interp1(v,xq)

vq = interp1(v,xq,method)

vq = interp1(v,xq,method,extrapolation)

pp = interp1(x,v,method,'pp')

说明

vq = interp1(x,v,xq) 使用线性插值返回一维函数在特定查询点的插入值。向量 x 包含样本点，v 包含对应值 v(x)。向量 xq 包含查询点的坐标。

如果您有多个在同一点坐标采样的数据集，则可以将 v 以数组的形式进行传递。数组 v 的每一列都包含一组不同的一维样本值。

示例

vq = interp1(x,v,xq,method) 指定备选插值方法：'linear'、'nearest'、'next'、'previous'、'pchip'、'cubic'、'v5cubic'、'makima' 或 'spline'。默认方法为 'linear'。

示例

vq = interp1(x,v,xq,method,extrapolation) 用于指定外插策略，来计算落在 x 域范围外的点。如果希望使用 method 算法进行外插，可将 extrapolation 设置为 'extrap'。您也可以指定一个标量值，这种情况下，interp1 将为所有落在 x 域范围外的点返回该标量值。

示例

vq = interp1(v,xq) 返回插入的值，并假定一个样本点坐标默认集。默认点是从 1 到 n 的数字序列，其中 n 取决于 v 的形状：

当 v 是向量时，默认点是 1:length(v)。
当 v 是数组时，默认点是 1:size(v,1)。

如果您不在意点之间的绝对距离，则可使用此语法。

示例

vq = interp1(v,xq,method) 指定备选插值方法中的任意一种，并使用默认样本点。

vq = interp1(v,xq,method,extrapolation) 指定外插策略，并使用默认样本点。

pp = interp1(x,v,method,'pp') 使用 method 算法返回分段多项式形式的 v(x)。

注意

不建议使用该语法。请改用 griddedInterpolant。

示例

全部折叠

基于粗略采样的正弦函数进行插值

打开实时脚本

定义样本点 x 及其对应样本值 v。

x = 0:pi/4:2*pi; 
v = sin(x);

将查询点定义为 x 范围内更精细的采样点。

xq = 0:pi/16:2*pi;

在查询点插入函数并绘制结果。

figure
vq1 = interp1(x,v,xq);
plot(x,v,'o',xq,vq1,':.');
xlim([0 2*pi]);
title('(Default) Linear Interpolation');

现在使用 'spline' 方法计算相同点处的 v。

figure
vq2 = interp1(x,v,xq,'spline');
plot(x,v,'o',xq,vq2,':.');
xlim([0 2*pi]);
title('Spline Interpolation');

在不指定样本点的情况下进行插值

打开实时脚本

定义一组函数值。

v = [0  1.41  2  1.41  0  -1.41  -2  -1.41 0];

定义一组介于默认点 1:9 之间的查询点。在这种情况下，默认点为 1:9，因为 v 包含 9 个值。

xq = 1.5:8.5;

计算 xq 处的 v。

vq = interp1(v,xq);

绘制结果。

figure
plot((1:9),v,'o',xq,vq,'*');
legend('v','vq');

复数值插值

打开实时脚本

定义一组样本点。

x = 1:10;

定义函数 $v (x) = 5 x + x^{2} i$ 在样本点处的值。

v = (5*x)+(x.^2*1i);

将查询点定义为 x 范围内更精细的采样点。

xq = 1:0.25:10;

在查询点处进行 v 插值。

vq = interp1(x,v,xq);

用红色绘制结果的实部，用蓝色绘制虚部。

figure
plot(x,real(v),'*r',xq,real(vq),'-r');
hold on
plot(x,imag(v),'*b',xq,imag(vq),'-b');

日期和时间的插值

打开实时脚本

对时间戳数据点进行插值。

以包含温度读数的数据集为例，这些读数每四个小时测量一次。创建包含一天的数据的表，并绘制数据图。

x = (datetime(2016,1,1):hours(4):datetime(2016,1,2))';
x.Format = 'MMM dd, HH:mm';
T = [31 25 24 41 43 33 31]';
WeatherData = table(x,T,'VariableNames',{'Time','Temperature'})

WeatherData=7×2 table
        Time         Temperature
    _____________    ___________

    Jan 01, 00:00        31     
    Jan 01, 04:00        25     
    Jan 01, 08:00        24     
    Jan 01, 12:00        41     
    Jan 01, 16:00        43     
    Jan 01, 20:00        33     
    Jan 02, 00:00        31

plot(WeatherData.Time, WeatherData.Temperature, 'o')

对数据集插值以预测一天中每一分钟内的温度读数。由于数据是周期性的，因此请使用 'spline' 插值方法。

xq = (datetime(2016,1,1):minutes(1):datetime(2016,1,2))';
V = interp1(WeatherData.Time, WeatherData.Temperature, xq, 'spline');

绘制插入的点。

hold on
plot(xq,V,'r')

使用两种不同方法进行外插

打开实时脚本

定义样本点 x 及其对应样本值 v。

x = [1 2 3 4 5];
v = [12 16 31 10 6];

指定查询点 xq，这些查询点延伸到 x 的定义域以外。

xq = [0 0.5 1.5 5.5 6];

使用 'pchip' 方法计算 xq 处的 v。

vq1 = interp1(x,v,xq,'pchip')

vq1 = 1×5

   19.3684   13.6316   13.2105    7.4800   12.5600

接着，使用 'linear' 方法计算 xq 处的 v。

vq2 = interp1(x,v,xq,'linear')

vq2 = 1×5

   NaN   NaN    14   NaN   NaN

现在将 'linear' 方法与 'extrap' 选项结合使用。

vq3 = interp1(x,v,xq,'linear','extrap')

vq3 = 1×5

     8    10    14     4     2

'pchip' 默认外插，但 'linear' 不会。

为 x 域范围外的所有查询指定常量值

打开实时脚本

定义样本点 x 及其对应样本值 v。

x = [-3 -2 -1 0 1 2 3];
v = 3*x.^2;

指定查询点 xq，这些查询点延伸到 x 的定义域以外。

xq = [-4 -2.5 -0.5 0.5 2.5 4];

现在使用 'pchip' 方法计算 xq 处的 v，并为 x 域范围外的所有查询点赋予值 27。

vq = interp1(x,v,xq,'pchip',27)

vq = 1×6

   27.0000   18.6562    0.9375    0.9375   18.6562   27.0000

在一个传递点插入多组数据

打开实时脚本

定义样本点。

x = (-5:5)';

在 x 所定义的点处对三个不同的抛物线函数采样。

v1 = x.^2;
v2 = 2*x.^2 + 2;
v3 = 3*x.^2 + 4;

创建矩阵 v，其列为向量 v1、v2 和 v3。

v = [v1 v2 v3];

将一组查询点 xq 定义为 x 范围内更精细的采样点。

xq = -5:0.1:5;

计算 xq 处的全部三个函数，并绘制结果。

vq = interp1(x,v,xq,'pchip');
figure
plot(x,v,'o',xq,vq);

h = gca;
h.XTick = -5:5;

绘图中的圆圈表示 v，实线表示 vq。

输入参数

全部折叠

`x` — 样本点
向量

样本点，指定为一行或一列实数向量。x 中的值必须各不相同。x 的长度必须符合以下要求之一：

如果 v 为向量，则 length(x) 必须等于 length(v)。
如果 v 为数组，则 length(x) 必须等于 size(v,1)。

示例: [1 2 3 4 5 6 7 8 9 10]

示例: 1:10

示例: [3 7 11 15 19 23 27 31]'

数据类型: single | double | duration | datetime

`v` — 样本值
向量 | 矩阵 | 数组

样本值，指定为实数/复数向量、矩阵或数组。如果 v 是矩阵或数组，则每列包含单独的一组一维值。

如果 v 包含复数，则 interp1 将分别对实部和虚部插值。

示例: rand(1,10)

示例: rand(10,1)

示例: rand(10,3)

数据类型: single | double | duration | datetime
复数支持: 是

`xq` — 查询点
标量 | 向量 | 矩阵 | 数组

查询点，指定为实数标量、向量、矩阵或数组。

示例: 5

示例: 1:0.05:10

示例: (1:0.05:10)'

示例: [0 1 2 7.5 10]

数据类型: single | double | duration | datetime

`method` — 插值方法
`'linear'` (默认) | `'nearest'` | `'next'` | `'previous'` | `'pchip'` | `'cubic'` | `'v5cubic'` | `'makima'` | `'spline'`

插值方法，指定为下表中的选项之一。

方法	描述	连续性	注释
`'linear'`	线性插值。查询点处的插入值基于各维中邻近网格点处数值的线性插值。这是默认插值方法。	C⁰	需要至少 2 个点。比最近邻点插值需要更多内存和计算时间。
`'nearest'`	最近邻点插值。查询点处的插入值是距样本网格点最近的值。	不连续	需要至少 2 个点。最低内存要求最快计算时间
`'next'`	下一个邻点插值。查询点处的插入值是下一个采样网格点的值。	不连续	需要至少 2 个点。内存要求和计算时间与 `'nearest'` 相同
`'previous'`	上一个邻点插值。查询点处的插入值是上一个采样网格点的值。	不连续	需要至少 2 个点。内存要求和计算时间与 `'nearest'` 相同
`'pchip'`	保形分段三次插值。查询点处的插入值基于邻近网格点处数值的保形分段三次插值。	C¹	需要至少 4 个点。比 `'linear'` 需要更多内存和计算时间
`'cubic'`	用于 MATLAB^® 5 的三次卷积。	C¹	需要至少 3 个点。点必须均匀间隔对于不规则间隔的数据，此方法会回退到 `'spline'` 插值内存要求和计算时间与 `'pchip'` 相似
`'v5cubic'`	与 `'cubic'` 相同。	C¹
`'makima'`	修正 Akima 三次 Hermite 插值。查询点处的插入值基于次数最大为 3 的多项式的分段函数。为防过冲，已修正 Akima 公式。	C¹	需要至少 2 个点。产生的波动比 `'spline'` 小，但不像 `'pchip'` 那样急剧变平计算成本高于 `'pchip'`，但通常低于 `'spline'` 内存要求与 `'spline'` 类似
`'spline'`	使用非节点终止条件的样条插值。查询点处的插入值基于各维中邻近网格点处数值的三次插值。	C²	需要至少 4 个点。比 `'pchip'` 需要更多内存和计算时间

`extrapolation` — 外插策略
`'extrap'` | 标量值

外插策略，指定为 'extrap' 或实数标量值。

如果希望 interp1 使用与内插所用相同的方法来计算落在域范围外的点，则指定 'extrap'。
如果希望 interp1 为落在域范围外的点返回一个特定常量值，则指定一个标量值。

默认行为取决于输入参量：

如果您指定 'pchip'、'spline' 或 'makima' 插值方法，则默认行为是 'extrap'。
任何其他方法都会为落在域范围外的查询点默认返回 NaN。

示例: 'extrap'

示例: 5

数据类型: char | string | single | double

输出参量

全部折叠

`vq` — 插入的值
标量 | 向量 | 矩阵 | 数组

插入的值，以标量、向量、矩阵或数组的形式返回。vq 的大小取决于 v 和 xq 的形状。

v 的形状	xq 的形状	Vq 的大小	示例
向量	向量	`size(xq)`	如果 `size(v) = [1 100]` 且 `size(xq) = [1 500]`，则 `size(vq) = [1 500]`。
向量	矩阵或 N 维数组	`size(xq)`	如果 `size(v) = [1 100]` 且 `size(xq) = [50 30]`，则 `size(vq) = [50 30]`。
矩阵或 N 维数组	向量	`[length(xq) size(v,2),...,size(v,n)]`	如果 `size(v) = [100 3]` 且 `size(xq) = [1 500]`，则 `size(vq) = [500 3]`。
矩阵或 N 维数组	矩阵或 N 维数组	`[size(xq,1),...,size(xq,n),... size(v,2),...,size(v,m)]`	如果 `size(v) = [4 5 6]` 且 `size(xq) = [2 3 7]`，则 `size(vq) = [2 3 7 5 6]`。

`pp` — 分段多项式
结构体

分段多项式，以可传递到 ppval 函数进行计算的结构体的形式返回。

详细信息

全部折叠

Akima 和样条插值

[1] 和 [2] 中所述的一维插值 Akima 算法执行三次插值以生成具有连续一阶导数 (C1) 的分段多项式。该算法保持斜率，避免平台区的波动。每当有三个或更多连续共线点时，就会出现平台区，算法将这些点用一条直线相连。为了确保两个数据点之间的区域是平坦的，请在这两个点之间插入一个额外的数据点。

当两个具有不同斜率的平台区相遇时，对原始 Akima 算法所做的修改会对斜率更接近于零的一侧赋予更多权重。此修改优先考虑更接近水平的一侧，这样更直观并可避免过冲。（原始 Akima 算法对两边的点赋予相等的权重，从而均匀地划分波动。）

另一方面，样条算法执行三次插值以产生具有连续二阶导数 (C2) 的分段多项式。结果相当于常规多项式插值，但不太容易受到高次数据点之间剧烈振荡的影响。但这种方法仍容易受到数据点之间的过冲和振荡的影响。

与样条算法相比，Akima 算法产生的波动较少，更适合处理平台区之间的快速变化。下面使用连接多个平台区的测试数据来说明这种差异。

参考

[1] Akima, Hiroshi. "A new method of interpolation and smooth curve fitting based on local procedures." Journal of the ACM (JACM) , 17.4, 1970, pp. 589-602.

[2] Akima, Hiroshi. "A method of bivariate interpolation and smooth surface fitting based on local procedures." Communications of the ACM , 17.1, 1974, pp. 18-20.

扩展功能

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

输入参量 x（样本点）必须严格递增或严格递减。索引不重新排序。
如果输入参量 v（样本值）为可变长度向量（1×: 或 :×1），则输出 vq 的形状与 MATLAB 中的形状相匹配。
如果输入参量 v 是可变大小，不是可变长度向量，并且在运行时变为行向量，则会发生错误。
如果采样值或查询点包含 Inf 或 -Inf，则生成的代码的输出可能与 MATLAB 中的输出不匹配。
如果输入参量 xq（查询点）是可变大小，不是可变长度向量，并且在运行时变为行或列向量，则会发生错误。
请参阅Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder)。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

用法说明和限制：

输入参量 x（样本点）必须严格递增或严格递减。索引不重新排序。
如果输入参量 v（样本值）为可变长度向量（1×: 或 :×1），则输出 vq 的形状与 MATLAB 中的形状相匹配。
如果输入参量 v 是可变大小，不是可变长度向量，并且在运行时变为行向量，则会发生错误。
如果输入参量 xq（查询点）是可变大小，不是可变长度向量，并且在运行时变为行或列向量，则会发生错误。
请参阅Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder)。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

用法说明和限制：

不支持插值方法 'pchip' 和 'makima'。
包含 NaN 的采样值 v 不支持 'spline' 插值方法。

有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

此函数完全支持分布式数组。有关详细信息，请参阅使用分布式数组运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

全部展开

R2020b: `interp1` 的 `'cubic'` 方法执行三次卷积

在 R2020b 中，interp1 的 'cubic' 插值方法执行三次卷积。'v5cubic' 和 'cubic' 插值方法现在执行相同类型的插值，这与 interp2、interp3 和 interpn 的行为一致。三次卷积插值方法适用于均匀间隔的数据，对于非均匀间隔的数据，它会回退到 'spline' 插值。

在以前的版本中，'cubic' 与 'pchip' 相同，只有 'v5cubic' 执行三次卷积。

另请参阅

interp2 | interp3 | interpn | griddedInterpolant

interp1

语法

说明

示例

基于粗略采样的正弦函数进行插值

在不指定样本点的情况下进行插值

复数值插值

日期和时间的插值

使用两种不同方法进行外插

为 x 域范围外的所有查询指定常量值

在一个传递点插入多组数据

输入参数

x — 样本点 向量

v — 样本值 向量 | 矩阵 | 数组

xq — 查询点 标量 | 向量 | 矩阵 | 数组

method — 插值方法 'linear' (默认) | 'nearest' | 'next' | 'previous' | 'pchip' | 'cubic' | 'v5cubic' | 'makima' | 'spline'

extrapolation — 外插策略 'extrap' | 标量值

输出参量

vq — 插入的值 标量 | 向量 | 矩阵 | 数组

pp — 分段多项式 结构体

详细信息

Akima 和样条插值

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成 使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组 使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

版本历史记录

R2020b: interp1 的 'cubic' 方法执行三次卷积

另请参阅

WeChat

`x` — 样本点
向量

`v` — 样本值
向量 | 矩阵 | 数组

`xq` — 查询点
标量 | 向量 | 矩阵 | 数组

`method` — 插值方法
`'linear'` (默认) | `'nearest'` | `'next'` | `'previous'` | `'pchip'` | `'cubic'` | `'v5cubic'` | `'makima'` | `'spline'`

`extrapolation` — 外插策略
`'extrap'` | 标量值

`vq` — 插入的值
标量 | 向量 | 矩阵 | 数组

`pp` — 分段多项式
结构体

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

R2020b: `interp1` 的 `'cubic'` 方法执行三次卷积