使用长短期记忆网络对 ECG 信号进行分类

此示例使用:

此示例说明如何使用深度学习和信号处理对来自 PhysioNet 2017 Challenge 的心电图 (ECG) 数据进行分类。具体而言，该示例使用长短期记忆网络和时频分析。

有关使用 GPU 和 Parallel Computing Toolbox™ 重现和加速此工作流的示例，请参阅Classify ECG Signals Using Long Short-Term Memory Networks with GPU Acceleration。

简介

ECG 记录一段时间内人体心脏的电活动。医生使用 ECG 检测患者的心跳是正常还是不规则。

心房纤维性颤动 (AFib) 是一种不规则的心跳，当心脏的上腔（即心房）与下腔（即心室）失去协调时就会发生心房纤维性颤动。

此示例使用的 ECG 数据来自 PhysioNet 2017 Challenge [1]、[2]、[3]，可从 https://physionet.org/challenge/2017/ 获得。数据由一组以 300 Hz 频率采样的 ECG 信号组成，由一组专家分成四个不同类：正常 (N)、AFib (A)、其他心律 (O) 和含噪记录 (~)。此示例说明如何使用深度学习来自动化分类过程。该过程使用一个二类分类器，该二类分类器可以将正常 ECG 信号和显示 AFib 符号的信号区分开来。

长短期记忆 (LSTM) 网络是一种循环神经网络 (RNN)，非常适合研究序列和时间序列数据。LSTM 网络可以学习序列的时间步之间的长期相关性。LSTM 层 (lstmLayer (Deep Learning Toolbox)) 可以前向分析时间序列，而双向 LSTM 层 (bilstmLayer (Deep Learning Toolbox)) 可以前向和后向分析时间序列。此示例使用双向 LSTM 层。

此示例说明在解决人工智能 (AI) 问题时使用以数据为中心的方法的优势。最初尝试使用原始数据训练 LSTM 网络得到的结果未达到标准。使用提取的特征训练相同的模型架构使分类性能得到显著提高。

为了加快训练过程，请在具有 GPU 的机器上运行此示例。如果您的机器同时有 GPU 和 Parallel Computing Toolbox™，则 MATLAB® 会自动使用 GPU 进行训练；否则，它使用 CPU。

加载并检查数据

运行 ReadPhysionetData 脚本，从 PhysioNet 网站下载数据，并生成包含适当格式的 ECG 信号的 MAT 文件 (PhysionetData.mat)。下载数据可能需要几分钟。使用一个条件语句，限定仅在当前文件夹中不存在 PhysionetData.mat 时才运行该脚本。

if ~isfile('PhysionetData.mat')
    ReadPhysionetData         
end
load PhysionetData

加载操作会向工作区添加两个变量：Signals 和 Labels。Signals 是保存 ECG 信号的元胞数组。Labels 是分类数组，它保存信号的对应真实值标签。

Signals(1:5)'

ans=1×5 cell array
    {1×9000 double}    {1×9000 double}    {1×18000 double}    {1×9000 double}    {1×18000 double}

Labels(1:5)'

ans = 1×5 categorical
     N      N      N      A      A

使用 summary 函数查看数据中包含多少 AFib 信号和正常信号。

summary(Labels)

Labels: 5788×1 categorical

     A                 738 
     N                5050 
     <undefined>         0

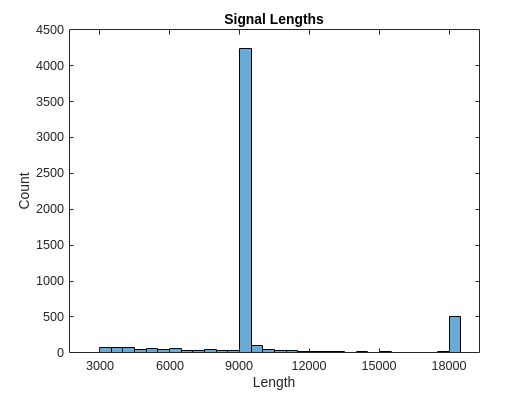
生成信号长度的直方图。大多数信号的长度是 9000 个采样。

L = cellfun(@length,Signals);
h = histogram(L);
xticks(0:3000:18000);
xticklabels(0:3000:18000);
title('Signal Lengths')
xlabel('Length')
ylabel('Count')

可视化每个类中一个信号的一段。AFib 心跳间隔不规则，而正常心跳会周期性发生。AFib 心跳信号还经常缺失 P 波，P 波在正常心跳信号的 QRS 复合波之前出现。正常信号的绘图会显示 P 波和 QRS 复合波。

normal = Signals{1};
aFib = Signals{4};

tiledlayout("flow")
nexttile
plot(normal)
title("Normal Rhythm")
xlim([4000,5200])
ylabel("Amplitude (mV)")
text(4330,150,"P",HorizontalAlignment="center")
text(4370,850,"QRS",HorizontalAlignment="center")

nexttile
plot(aFib)
title("Atrial Fibrillation")
xlim([4000,5200])
xlabel("Samples")
ylabel("Amplitude (mV)")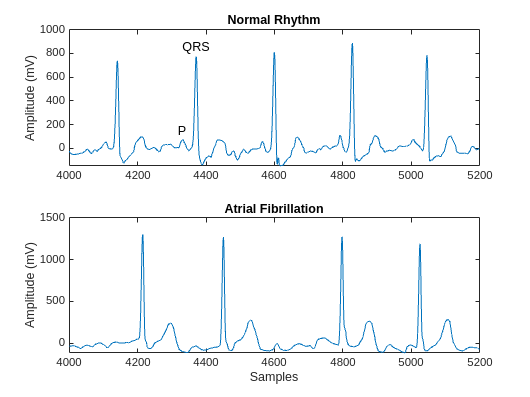

准备要训练的数据

在训练期间，trainnet 函数将数据分成小批量。然后，该函数在同一个小批量中填充或截断信号，使它们都具有相同的长度。过多的填充或截断会对网络性能产生负面影响，因为网络可能会根据添加或删除的信息错误地解释信号。

为避免过度填充或截断，请对 ECG 信号应用 helperSegmentSignals 函数，使它们的长度都为 9000 个采样。该 helperSegmentSignals 函数在此示例的末尾定义。该函数会忽略少于 9000 个采样的信号。如果信号的采样超过 9000 个，helperSegmentSignals 会将其分成尽可能多的包含 9000 个采样的信号段，并忽略剩余采样。例如，具有 18500 个采样的信号将变为两个包含 9000 个采样的信号，剩余的 500 个采样被忽略。

[Signals,Labels] = helperSegmentSignals(Signals,Labels);

查看 Signals 数组的前五个元素，以验证每个条目的长度现在为 9000 个采样。

Signals(1:5)'

ans=1×5 cell array
    {1×9000 double}    {1×9000 double}    {1×9000 double}    {1×9000 double}    {1×9000 double}

第一次尝试：使用原始信号数据训练分类器

要设计分类器，请使用上一节中生成的原始信号。将信号分成一个训练集（用于训练分类器）和一个测试集（用于基于新数据测试分类器的准确度）。

使用 summary 函数显示 AFib 信号与正常信号的比率约为 1:7。

summary(Labels)

Labels: 5655×1 categorical

     A                 718 
     N                4937 
     <undefined>         0

由于约 7/8 的信号是正常信号，因此分类器会发现通过简单地将所有信号分类为正常信号就可达到高准确度。为了避免这种偏置，需要通过复制数据集中的 AFib 信号来增加 AFib 数据，以便正常信号和 AFib 信号的数量相同。这种复制通常称为过采样，是深度学习中使用的一种数据增强形式。

根据信号所属的类划分信号。

afibX = Signals(Labels=="A");
afibY = Labels(Labels=="A");

normalX = Signals(Labels=="N");
normalY = Labels(Labels=="N");

接下来，使用 splitlabels 将每个类的目标随机分为训练集、验证集和测试集。

rng("default")

indA = splitlabels(afibY,[0.8 0.1],"randomized");
indN = splitlabels(normalY,[0.8 0.1],"randomized");

XTrainA = afibX(indA{1});
YTrainA = afibY(indA{1});
XTrainN = normalX(indN{1});
YTrainN = normalY(indN{1});

XValidA = afibX(indA{2});
YValidA = afibY(indA{2});
XValidN = normalX(indN{2});
YValidN = normalY(indN{2});

XTestA = afibX(indA{3});
YTestA = afibY(indA{3});
XTestN = normalX(indN{3});
YTestN = normalY(indN{3});

数据集不平衡。要获得相似数量的 AFib 信号和正常信号，请重复七次 AFib 信号。

默认情况下，神经网络会在训练前随机对数据进行乱序处理，以确保相邻信号不都有相同的标签。

XTrain = [repmat(XTrainA,7,1); XTrainN];
YTrain = [repmat(YTrainA,7,1); YTrainN];

XValid = [repmat(XValidA,7,1); XValidN];
YValid = [repmat(YValidA,7,1); YValidN];

XTest = [repmat(XTestA,7,1); XTestN];
YTest = [repmat(YTestA,7,1); YTestN];

现在，正常信号和 AFib 信号在训练集、验证集和测试集中均衡分布。

summary(YTrain)

YTrain: 7968×1 categorical

     A                4018 
     N                3950 
     <undefined>         0

summary(YValid)

YValid: 997×1 categorical

     A                504 
     N                493 
     <undefined>        0

summary(YTest)

YTest: 998×1 categorical

     A                504 
     N                494 
     <undefined>        0

定义 LSTM 网络架构

LSTM 网络可以学习序列数据的时间步之间的长期相关性。此示例使用双向 LSTM 层 bilstmLayer，因为它前向和后向检测序列。

由于输入信号各有一个维度，将输入大小指定是大小为 1 的序列。指定输出大小为 50 的一个双向 LSTM 层，并输出序列的最后一个元素。此命令指示双向 LSTM 层将输入时间序列映射到 50 个特征，然后为全连接层准备输出。最后，通过包含大小为 2 的全连接层并后跟一个 softmax 层，指定两个类。

layers = [ ...
    sequenceInputLayer(1)
    bilstmLayer(50,OutputMode="last")
    fullyConnectedLayer(2)
    softmaxLayer]

layers = 
  4×1 Layer array with layers:

     1   ''   Sequence Input    Sequence input with 1 dimensions
     2   ''   BiLSTM            BiLSTM with 50 hidden units
     3   ''   Fully Connected   2 fully connected layer
     4   ''   Softmax           softmax

接下来指定分类器的训练选项。在选项中进行选择需要经验分析。要通过运行试验探索不同训练选项配置，您可以使用Experiment Manager (Deep Learning Toolbox)。

使用 Adam 优化器进行训练。与默认的具有动量的随机梯度下降 (SGDM) 求解器相比，Adam 在使用 LSTM 之类的 RNN 时性能更好。
使用 200 的小批量大小进行 50 轮训练。
将梯度阈值设置为 1 以稳定训练。
每轮训练都会打乱数据。
指定验证数据。
由于训练数据具有行和列分别对应于通道和时间步的序列，请指定输入数据格式 'CTB'（通道、时间、批量）。
在图中显示训练进度，并在训练过程中监控网络的准确度。
禁用详尽输出。

options = trainingOptions("adam", ...
    MaxEpochs=50, ...
    MiniBatchSize=200, ...
    GradientThreshold=1, ...
    Shuffle="every-epoch", ...
    InitialLearnRate=1e-3, ...
    plots="training-progress", ...
    Metrics="accuracy", ...
    InputDataFormats="CTB", ...
    ValidationData={XValid,YValid}, ...
    OutputNetwork="best-validation", ...
    Verbose=false);

训练 LSTM 网络

通过使用 trainnet (Deep Learning Toolbox) 用指定的训练选项和层架构训练 LSTM 网络。对于分类，使用交叉熵损失。默认情况下，trainnet 函数使用 GPU（如果有）。在 GPU 上进行训练需要 Parallel Computing Toolbox™ 许可证和受支持的 GPU 设备。有关受支持设备的信息，请参阅GPU 计算要求 (Parallel Computing Toolbox)。否则，trainnet 函数使用 CPU。要指定执行环境，请使用 ExecutionEnvironment 训练选项。由于训练集很大，训练过程可能需要几分钟。默认情况下，如果您指定验证数据，则 trainnet 函数会返回验证损失最低的网络。

net = trainnet(XTrain,YTrain,layers,"crossentropy",options);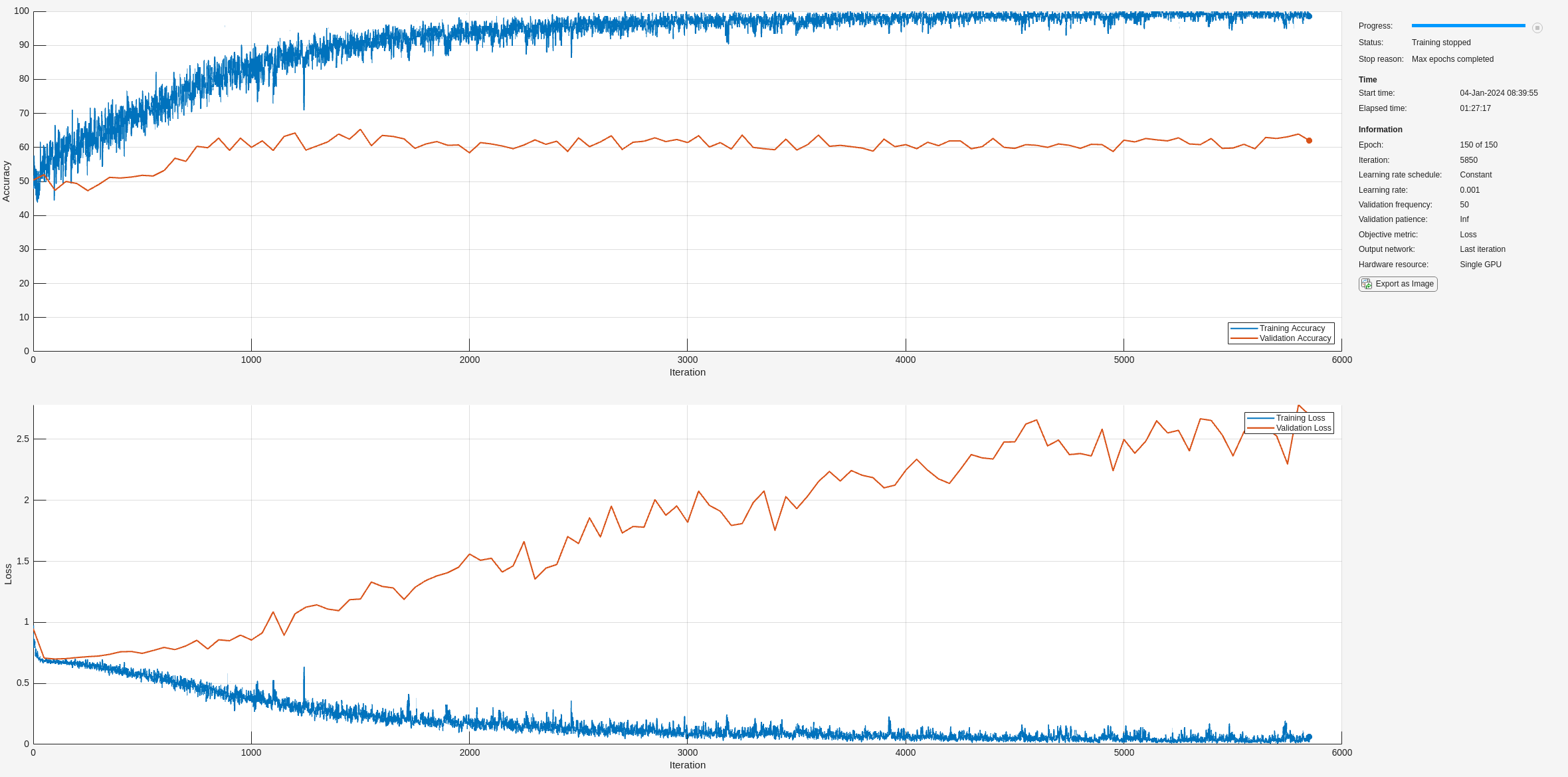

训练进度图的顶部子图表示训练准确度，即基于每个小批量的分类准确度。当训练在成功进行时，此值通常会逐渐增大，直到 100%。底部子图显示训练损失，即基于每个小批量的交叉熵损失。当训练在成功进行时，该值通常会逐渐降低，直到为零。

如果训练未收敛，绘图可能会在各值之间振荡，而不会呈现向上或向下趋势。这种振荡意味着训练准确度没有提高，训练损失没有减少。这种情况可能发生在训练开始时，或者在训练准确度有初步提高后，绘图可能趋于平稳。在许多情况下，更改训练选项可以帮助网络实现收敛。减少 MiniBatchSize 或减少 InitialLearnRate 可能会导致更长的训练时间，但这可能有助于网络更好地学习。

在此处，训练准确度很高，但验证准确度并没有相应提高。这可能指示过拟合，意味着模型无法泛化，而是与训练数据集过于接近。原因可能有很多，例如训练数据包含大量冗余和无关信息，以及网络没有学习到分类所需的真正关键因素。

可视化训练和测试准确度

计算训练准确度，该准确度表示分类器对于所训练信号的准确度。首先，对训练数据进行分类。

要使用多个观测值进行预测，请使用 minibatchpredict (Deep Learning Toolbox) 函数。要将预测分数转换为标签，请使用 scores2label 函数。minibatchpredict 函数自动使用 GPU（如果有）。否则，该函数使用 CPU。

classNames = categories(YTrain);
scores = minibatchpredict(net,XTrain,InputDataFormats="CTB");
trainPred = scores2label(scores,classNames);

在分类问题中，混淆矩阵用于可视化分类器对于一组已知真实数值的数据上的性能。目标类是信号的真实值标签，输出类是网络分配给信号的标签。坐标区标签表示类标签 AFib (A) 和 Normal (N)。

使用 confusionchart 命令计算用于测试数据预测的总体分类准确度。将 RowSummary 指定为 "row-normalized" 以在行汇总中显示真正率和假正率。此外，将 ColumnSummary 指定为 "column-normalized" 以在列汇总中显示正预测值和假发现率。

LSTMAccuracy = sum(trainPred == YTrain)/numel(YTrain)*100

LSTMAccuracy = 
58.8730

figure
confusionchart(YTrain,trainPred,ColumnSummary="column-normalized",...
              RowSummary="row-normalized",title="Confusion Chart for LSTM");

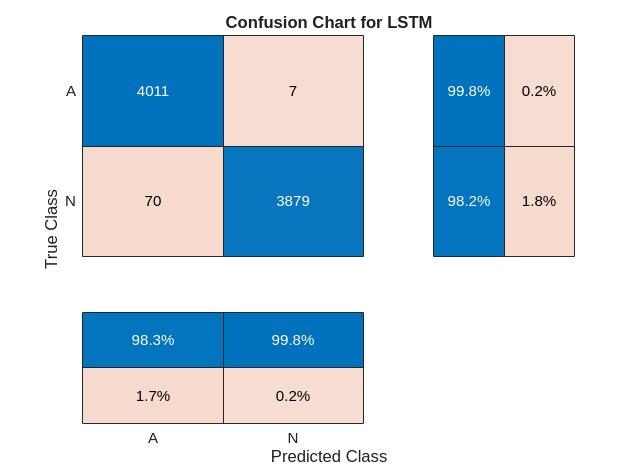
现在用相同的网络对测试数据进行分类。

scores = minibatchpredict(net,XTest,InputDataFormats="CTB");
testPred = scores2label(scores,classNames);

计算测试准确度，并使用混淆矩阵将分类性能可视化。

LSTMAccuracy = sum(testPred == YTest)/numel(YTest)*100

LSTMAccuracy = 
51.0020

figure
confusionchart(YTest,testPred,ColumnSummary="column-normalized",...
              RowSummary="row-normalized",Title="Confusion Chart for LSTM");

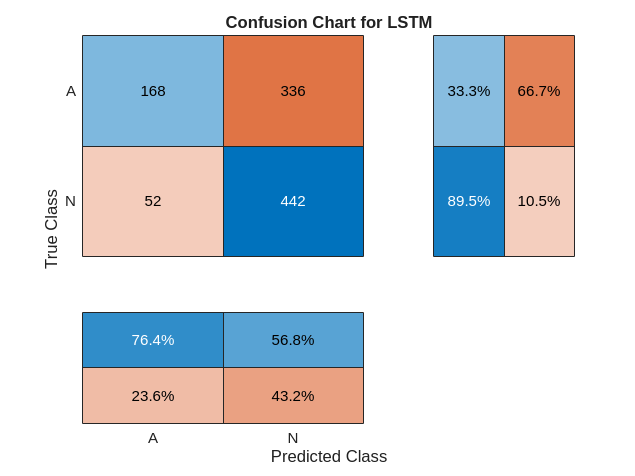
第二次尝试：通过特征提取提高性能

从数据中提取特征有助于提高分类器的性能。为了决定提取哪些特征，本示例采用的方法是先计算时频图像（如频谱图），然后使用它们来训练卷积神经网络 (CNN) [4]、[5]。

可视化每个信号类型的频谱图。

fs = 300;

figure
tiledlayout("flow")
nexttile
pspectrum(normal,fs,"spectrogram",TimeResolution=0.5)
title("Normal Signal")

nexttile
pspectrum(aFib,fs,"spectrogram",TimeResolution=0.5)
title("AFib Signal")

因为本示例使用 LSTM 而不是 CNN，必须转换该方法以应用于一维信号。时频 (TF) 矩从频谱图中提取信息。每个矩都可以用作一维特征以输入到 LSTM。

探查时域中的两个 TF 矩：

瞬时频率 (instfreq)
谱熵 (pentropy)

instfreq 函数估计信号的时变频率，作为功率谱图的第一个矩。该函数使用时间窗上的短时傅里叶变换计算频谱图。在本示例中，该函数使用 255 个时间窗。该函数的时间输出对应于时间窗的中心。

可视化每个信号类型的瞬时频率。

[instFreqA,tA] = instfreq(aFib,fs);
[instFreqN,tN] = instfreq(normal,fs);

figure
tiledlayout("flow")
nexttile
plot(tN,instFreqN)
title("Normal Signal")
xlabel("Time (s)")
ylabel("Instantaneous Frequency")

nexttile
plot(tA,instFreqA)
title("AFib Signal")
xlabel("Time (s)")
ylabel("Instantaneous Frequency")

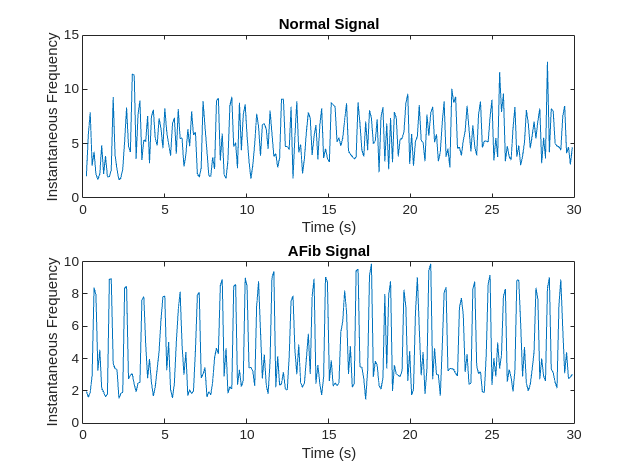
使用 cellfun 将 instfreq 函数应用于训练集中和测试集中的每个单元。

instfreqTrain = cellfun(@(x)instfreq(x,fs)',XTrain,UniformOutput=false);
instfreqTest = cellfun(@(x)instfreq(x,fs)',XTest,UniformOutput=false);
instfreqValid = cellfun(@(x)instfreq(x,fs)',XValid,UniformOutput=false);

谱熵测量信号的频谱的尖度或平坦度。具有尖峰频谱的信号（如正弦波之和）具有低谱熵。具有平坦频谱的信号（如白噪声）具有高谱熵。spectralEntropy 函数基于功率谱估计谱熵。这与瞬时频率估计情况一样。

[s,f,tA2] = pspectrum(aFib,fs,"spectrogram");
pentropyA = spectralEntropy(s,f,Scaled=true);
[s,f,tN2] = pspectrum(normal,fs,"spectrogram");
pentropyN = spectralEntropy(s,f,Scaled=true);

可视化每个信号类型的谱熵。

figure
tiledlayout("flow")
nexttile
plot(tN2,pentropyN)
title("Normal Signal")
ylabel("Spectral Entropy")

nexttile
plot(tA2,pentropyA)
title("AFib Signal")
xlabel("Time (s)")
ylabel("Spectral Entropy")

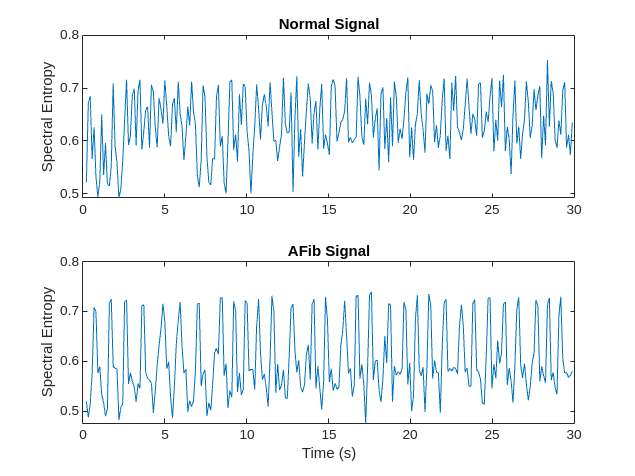
使用 cellfun 将 helperComputeSpecEntropy 函数应用于训练集、测试集和验证集中的每个单元。

pentropyTrain = cellfun(@(x)helperComputeSpecEntropy(x,fs)',XTrain,UniformOutput=false);
pentropyTest = cellfun(@(x)helperComputeSpecEntropy(x,fs)',XTest,UniformOutput=false);
pentropyValid = cellfun(@(x)helperComputeSpecEntropy(x,fs)',XValid,UniformOutput=false);

串联这些特征，使新的训练集和测试集中的每个单元都有两个维度（即两个特征）。

XTrain2 = cellfun(@(x,y)[x;y],instfreqTrain,pentropyTrain,UniformOutput=false);
XTest2 = cellfun(@(x,y)[x;y],instfreqTest,pentropyTest,UniformOutput=false);
XValid2 = cellfun(@(x,y)[x;y],instfreqValid,pentropyValid,UniformOutput=false);

可视化新输入的格式。每个单元不再包含一个长度为 9000 个采样的信号；现在它包含两个长度为 255 个采样的特征。

XTrain2(1:5)'

ans=1×5 cell array
    {2×255 double}    {2×255 double}    {2×255 double}    {2×255 double}    {2×255 double}

标准化数据

瞬时频率和谱熵的均值相差几乎一个数量级。而且，瞬时频率均值可能太高，以致 LSTM 无法高效学习。当网络适合于均值和极差较大的数据时，大的输入可能会减慢网络的学习和收敛速度 [6]。

mean(instFreqN)

ans = 
5.5551

mean(pentropyN)

ans = 
0.6324

使用训练集均值和标准差来标准化训练集、测试集和验证集。标准化，或 z 分数，是一种在训练过程中提高网络性能的常用方法。

XV = [XTrain2{:}];
mu = mean(XV,2);
sg = std(XV,[],2);

XTrainSD = XTrain2;
XTrainSD = cellfun(@(x)(x-mu)./sg,XTrainSD,UniformOutput=false);
XValidSD = XValid2;
XValidSD = cellfun(@(x)(x-mu)./sg,XValidSD,UniformOutput=false);
XTestSD = XTest2;
XTestSD = cellfun(@(x)(x-mu)./sg,XTestSD,UniformOutput=false);

显示标准化瞬时频率和谱熵的均值。

instFreqNSD = XTrainSD{1}(1,:);
pentropyNSD = XTrainSD{1}(2,:);

mean(instFreqNSD)

ans = 
0.1545

mean(pentropyNSD)

ans = 
0.1936

修改 LSTM 网络架构

现在每个信号都有两个维度，就有必要通过将输入序列大小指定为 2 来修改网络架构。指定一个具有 50 个隐藏单元的双向 LSTM 层，并输出序列的最后一个元素。通过包含大小为 2 的全连接层并后跟一个 softmax 层，指定两个类。

layers = [ ...
    sequenceInputLayer(2)
    bilstmLayer(50,OutputMode="last")
    fullyConnectedLayer(2)
    softmaxLayer]

layers = 
  4×1 Layer array with layers:

     1   ''   Sequence Input    Sequence input with 2 dimensions
     2   ''   BiLSTM            BiLSTM with 50 hidden units
     3   ''   Fully Connected   2 fully connected layer
     4   ''   Softmax           softmax

指定训练选项。训练选项与用于训练第一个网络的选项相同，不同之处在于进行 150 轮训练而不是 50 轮，并指定不同的验证数据。

options = trainingOptions("adam", ...
    MaxEpochs=150, ...
    MiniBatchSize=200, ...
    GradientThreshold=1, ...
    Shuffle="every-epoch", ...
    InitialLearnRate=1e-3, ...
    plots="training-progress", ...
    Metrics="accuracy", ...
    InputDataFormats="CTB", ...
    ValidationData={XValidSD,YValid}, ...
    OutputNetwork="best-validation", ...
    Verbose=false);

用时频特征训练 LSTM 网络

通过使用 trainnet 用指定的训练选项和层架构训练 LSTM 网络。

net2 = trainnet(XTrainSD,YTrain,layers,"crossentropy",options);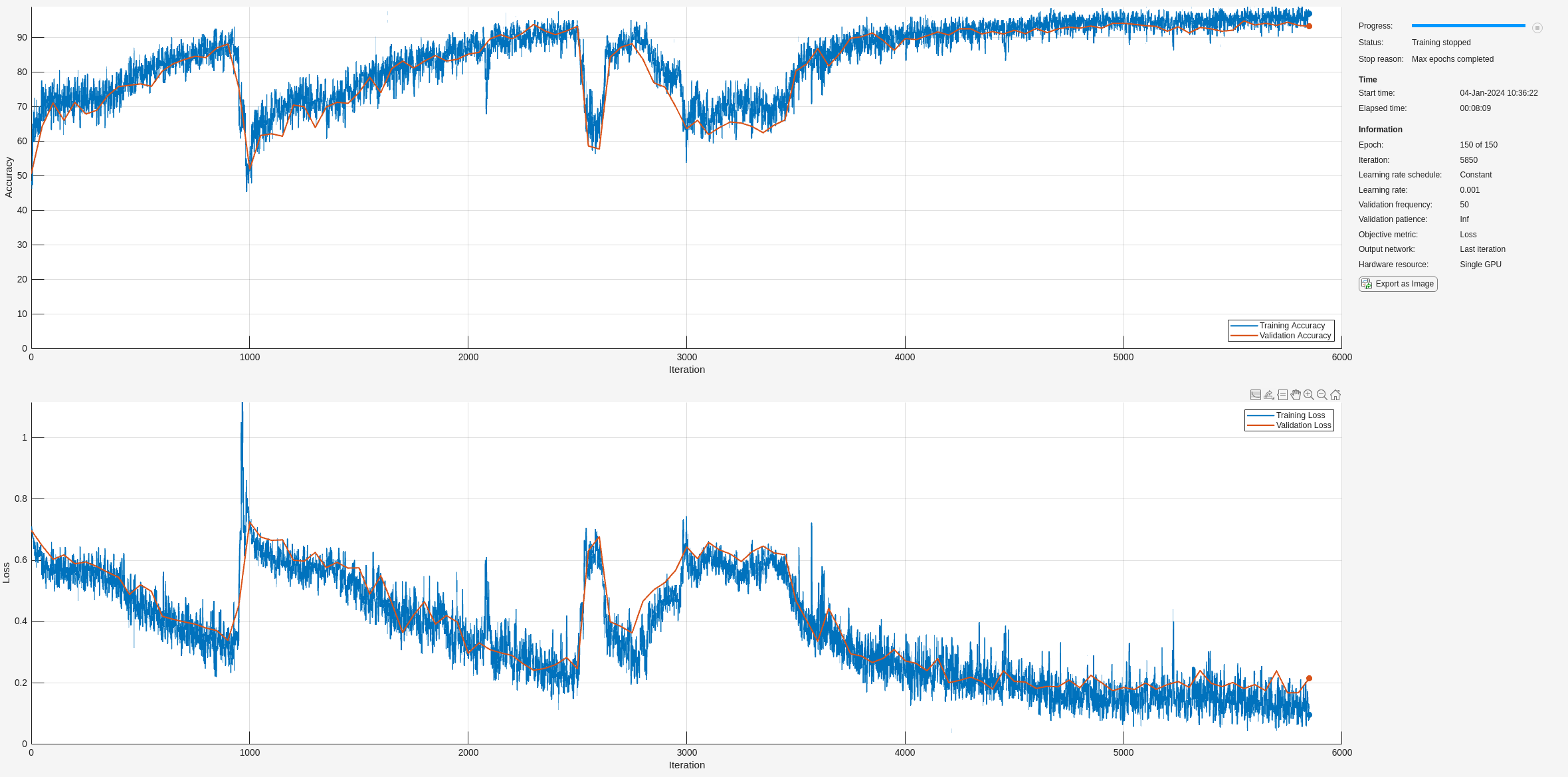

训练所需的时间减少，因为 TF 矩比原始序列短。

可视化训练和测试准确度

使用更新后的 LSTM 网络对训练数据进行分类。将分类性能可视化为混淆矩阵。

scores = minibatchpredict(net2,XTrainSD,InputDataFormats="CTB");
trainPred2 = scores2label(scores,classNames);
LSTMAccuracy = sum(trainPred2 == YTrain)/numel(YTrain)*100

LSTMAccuracy = 
95.5447

figure
confusionchart(YTrain,trainPred2,ColumnSummary="column-normalized",...
              RowSummary="row-normalized",Title="Confusion Chart for LSTM");

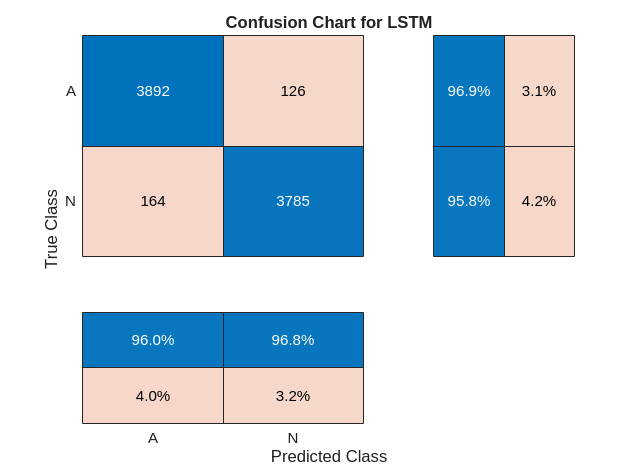
使用更新后的网络对测试数据进行分类。绘制混淆矩阵以检查测试准确度。

scores = minibatchpredict(net2,XTestSD,InputDataFormats="CTB");
testPred2 = scores2label(scores,classNames);
LSTMAccuracy = sum(testPred2 == YTest)/numel(YTest)*100

LSTMAccuracy = 
94.7896

figure
confusionchart(YTest,testPred2,ColumnSummary="column-normalized",...
              RowSummary="row-normalized",Title="Confusion Chart for LSTM");

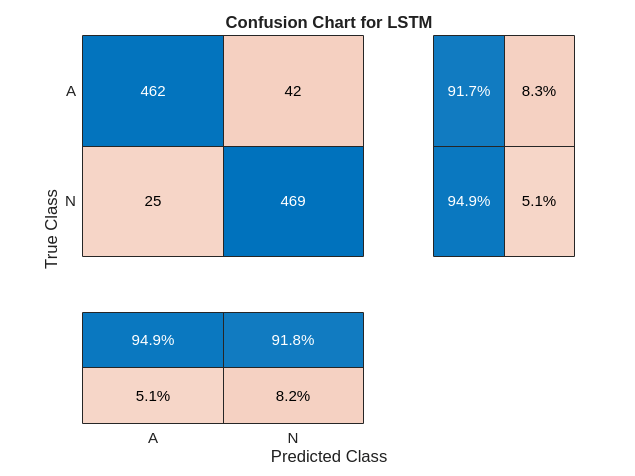
结论

此示例说明如何使用 LSTM 网络构建分类器来检测 ECG 信号中的心房颤动。该过程使用过采样来避免在主要由健康被测者组成的人群中检测异常情况时出现的分类偏置。使用原始信号数据训练 LSTM 网络会导致分类准确度差。对每个信号使用两个时频矩特征来训练网络可显著提高分类性能，同时减少训练时间。

参考资料

[1] AF Classification from a Short Single Lead ECG Recording: the PhysioNet/Computing in Cardiology Challenge, 2017. https://physionet.org/challenge/2017/

[2] Clifford, Gari, Chengyu Liu, Benjamin Moody, Li-wei H. Lehman, Ikaro Silva, Qiao Li, Alistair Johnson, and Roger G. Mark."AF Classification from a Short Single Lead ECG Recording:The PhysioNet Computing in Cardiology Challenge 2017."Computing in Cardiology (Rennes:IEEE).Vol. 44, 2017, pp. 1–4.

[3] Goldberger, A. L., L. A. N. Amaral, L. Glass, J. M. Hausdorff, P. Ch.Ivanov, R. G. Mark, J. E. Mietus, G. B. Moody, C.-K. Peng, and H. E. Stanley."PhysioBank, PhysioToolkit, and PhysioNet:Components of a New Research Resource for Complex Physiologic Signals".Circulation.Vol. 101, No. 23, 13 June 2000, pp. e215–e220. http://circ.ahajournals.org/content/101/23/e215.full

[4] Pons, Jordi, Thomas Lidy, and Xavier Serra."Experimenting with Musically Motivated Convolutional Neural Networks".14th International Workshop on Content-Based Multimedia Indexing (CBMI).June 2016.

[5] Wang, D."Deep learning reinvents the hearing aid," IEEE Spectrum, Vol. 54, No. 3, March 2017, pp. 32–37. doi:10.1109/MSPEC.2017.7864754.

[6] Brownlee, Jason.How to Scale Data for Long Short-Term Memory Networks in Python.7 July 2017. https://machinelearningmastery.com/how-to-scale-data-for-long-short-term-memory-networks-in-python/.

附录 - 辅助函数

helperSegmentSignals - 此函数接受由 ECG 信号组成的元胞数组 signalsIn 和由标签组成的元胞数组 labelsIn。为避免过度填充或截断，此函数对每个信号进行分段，忽略少于 9000 个采样的信号，并将剩余信号分成尽可能多的包含 9000 个采样的信号段，忽略任何剩余采样。例如，具有 18500 个采样的信号将变为两个包含 9000 个采样的信号，剩余的 500 个采样被忽略。如果此函数将信号分成若干包含 9000 个采样的信号段，则此函数会使用原始信号的标签标记每个段。

function [signalsOut,labelsOut] = helperSegmentSignals(signalsIn,labelsIn)
% This functions is only for use in this example. It might change or be removed in a future release.

% Specify the length of each segmented signal.
targetLength = 9000;

signalsOut = {};
labelsOut = {};

for idx = 1:numel(signalsIn)
    
    % Extract signal and label from cell array.
    x = signalsIn{idx};
    y = labelsIn(idx);
    
    % Skip signals shorter than 9000 samples.
    if length(x) < targetLength
        continue;
    end

    % Partition signal into frames of length 9000.
    x = framesig(x,targetLength);
    
    % Compute the number of targetLength-sample chunks in the signal.
    numSigs = size(x,2);

    % Repeat the label numSigs times.
    y = repmat(y,[numSigs,1]);

    % Vertically concatenate into cell arrays.
    signalsOut = [signalsOut; mat2cell(x.',ones(numSigs,1))]; %#ok<AGROW>
    labelsOut = [labelsOut; cellstr(y)]; %#ok<AGROW>
end

% Convert labels to categorical.
labelsOut = categorical(labelsOut);

end

helperComputeSpecEntropy - 此函数计算谱熵。

function [specentropy,t] = helperComputeSpecEntropy(signal,fs)
    [s,f,t] = pspectrum(signal,fs,"spectrogram");
    specentropy = spectralEntropy(s,f,Scaled=true);
end

另请参阅

函数

instfreq | pentropy | trainingOptions (Deep Learning Toolbox) | trainnet (Deep Learning Toolbox) | bilstmLayer (Deep Learning Toolbox) | lstmLayer (Deep Learning Toolbox)

主题

长短期记忆神经网络 (Deep Learning Toolbox)