Human Activity Recognition Using Signal Feature Extraction and Machine Learning

Data Set

The Sensor HAR (human activity recognition) App [1] was used to collect raw accelerometer signals in [2]. The smartphone was worn by a subject during five different types of physical activity. The data set was then buffered to obtain 44 sample-long signals corresponding to a particular activity. The Dancing activity from the data set and the accelerometer signals in the y and z directions were excluded to create the BufferedHumanActivity data set stored in the BufferedHumanActivity.mat file used in this example.

Load the BufferedHumanActivity data set.

load BufferedHumanActivity.mat

The data set contains 7776 x-direction accelerometer signals. Each signal has a duration of 44 samples and corresponds to one of four different physical human activities: Sitting, Standing, Walking and Running. The data set contains the following variables:

Feature Extraction

The accelerometer signals may be thought of as containing two main components, one consisting of "fast" variations over time caused by body dynamics (physical movements of the subject). The other consisting of "slow" variations over time caused by the position of the body with respect to the vertical gravitational field.

To isolate the rapid signal variations from the slower ones, we apply a high pass filter to the original signals. We extract different features from the filtered and unfiltered signals using the signalTimeFeatureExtractor and signalFrequencyFeatureExtractor objects. These objects allow performant computation of multiple features in the time and frequency domains with one function call.

% Filter the signals with a highpass filter
atxFiltered = highpass(atx,0.7,fs);

For time features, two signalTimeFeatureExtractor objects are configured. One is used to extract the mean of the unfiltered signals (meanFE) and the second is used to extract the root mean square, shape factor, peak value, crest factor, clearance factor, and impulse factor of the filtered signals (timeFE).

meanFE = signalTimeFeatureExtractor("Mean",true,"SampleRate",fs);
timeFE = signalTimeFeatureExtractor("RMS",true,...
    "ShapeFactor",true,...
    "PeakValue",true,...
    "CrestFactor",true,...
    "ClearanceFactor",true,...    
    "ImpulseFactor",true,...
    "SampleRate",fs);

For frequency features, signalFrequencyFeatureExtractor is used to extract the mean frequency, band power, half-power bandwidth, peak amplitude and peak location of the filtered signals.

freqFE = signalFrequencyFeatureExtractor("PeakAmplitude",true,...
    "PeakLocation",true,...
    "MeanFrequency",true,...
    "BandPower",true,...
    "PowerBandwidth",true,...
    "SampleRate",fs);

The computation of spectral peaks can be refined by setting more parameters. For instance, the maximum number of peaks is set to 6, and the minimum distance between each spectral peak is set to 0.25Hz. Additionally, we choose an FFT length of 256 and a rectangular window of 44 samples (i.e., the signal length) to compute the spectral estimates.

fftLength = 256;
window = rectwin(size(atx,1));
setExtractorParameters(freqFE,"WelchPSD","FFTLength",fftLength,"Window",window);
mindist_xunits = 0.25;
minpkdist = floor(mindist_xunits/(fs/fftLength));
setExtractorParameters(freqFE,"PeakAmplitude","MaxNumExtrema",6,"MinSeparation",minpkdist);
setExtractorParameters(freqFE,"PeakLocation","MaxNumExtrema",6,"MinSeparation",minpkdist);

The computation of features for all the signals can be parallelized using transformed array datastores. The datastores read each matrix column and compute features using the extract function of the feature extractor objects.

meanFeatureDs = arrayDatastore(atx,"IterationDimension",2);
meanFeatureDs = transform(meanFeatureDs,@(x)meanFE.extract(x{:}));
timeFeatureDs = arrayDatastore(atxFiltered,"IterationDimension",2);
timeFeatureDs = transform(timeFeatureDs,@(x)timeFE.extract(x{:}));
freqFeatureDs = arrayDatastore(atxFiltered,"IterationDimension",2);
freqFeatureDs = transform(freqFeatureDs,@(x)freqFE.extract(x{:}));

Call the readall method of transformed datastore with the "UseParallel" option set to true to distribute the computations across a pool of workers if Parallel Computing Toolbox is installed. The resulting computed features are combined to end up with 22 features for each one of the 7776 signal observations.

meanFeatures = readall(meanFeatureDs,"UseParallel",true);
timeFeatures = readall(timeFeatureDs,"UseParallel",true);
freqFeatures = readall(freqFeatureDs,"UseParallel",true);

features = [meanFeatures timeFeatures freqFeatures];

Train an SVM Classifier Using Extracted Features

You can import the features and activity labels into the Classification Learner app to train an SVM classifier. Alternatively, you can create an SVM template and classifier using a feature table containing the features (predictors) and the activity labels (response) as follows.

First create a table with predictors and response.

featureTable = array2table(features);
actioncats = categorical(actnames)';
featureTable.ActivityID = actioncats(actid);
head(featureTable)

    features1    features2    features3    features4    features5    features6    features7    features8    features9    features10    features11    features12    features13    features14    features15    features16    features17    features18    features19    features20    features21    features22    ActivityID
    _________    _________    _________    _________    _________    _________    _________    _________    _________    __________    __________    __________    __________    __________    __________    __________    __________    __________    __________    __________    __________    __________    __________

     -73.408      0.10678      1.2695       0.24501      2.2946       3.5282        2.913       3.1208       0.011402     0.22658      0.0037348     0.0043388      0.0049913      0.014314    0.0032949     0.0042457      0.74219        1.6797        3.2031        3.8281        4.2188        4.5703       Sitting  
      -73.43      0.06735      1.2521       0.13304      1.9753       2.9553       2.4733       1.8959       0.004536     0.18083      0.0078615      0.001071      0.0046553     0.0023938    0.0017709      0.002039      0.74219          1.25        1.5625        2.3438        3.5938        3.9453       Sitting  
      -73.41       0.0626       1.303       0.15569       2.487       3.9603       3.2407       2.4191      0.0039188     0.18783      0.0036916      0.001265     0.00086816    0.00098286    0.0029621     0.0044119      0.74219        1.4062        2.2266        2.7734        3.0859        4.6094       Sitting  
     -73.393     0.072056      1.3457       0.20023      2.7788       4.6384       3.7394       2.9361       0.005192     0.21444      0.0028194     0.0016623      0.0028484     0.0018433     0.003666     0.0026144      0.89844        1.6797        2.3047        3.2422        4.0234        4.6484       Sitting  
     -73.409     0.080133      1.3786       0.21548       2.689        4.602       3.7069       3.2548      0.0064214      0.2053      0.0035392     0.0015361      0.0061205     0.0010848    0.0072086     0.0055945       1.5625        2.3828        3.0469        3.5156        3.8672        4.6484       Sitting  
      -73.43     0.071148      1.1902       0.13832      1.9441       2.6268       2.3139       3.0519      0.0050621     0.25175      0.0022982     0.0027692      0.0040954     0.0045089    0.0016846      0.003589      0.82031        2.3047        3.1641        3.9062        4.2188        4.5312       Sitting  
     -73.441     0.091667       1.169       0.19139      2.0879       2.7515       2.4408       2.8127      0.0084028     0.25907      0.0021497     0.0029254      0.0035706     0.0018514     0.015439     0.0030516      0.89844        2.1094        2.3828        2.6562        3.0859        4.5703       Sitting  
     -73.419      0.10858      1.1976       0.20506      1.8886       2.5625       2.2619       2.3954       0.011789     0.17288       0.010823     0.0088772      0.0078451     0.0071845    0.0066219     0.0024052      0.74219        1.5625        2.2656        3.0469        3.8281        4.5312       Sitting  

Partition the dataset by assigning 75% of the signals for training and 25% for testing. Use the cvpartition function to ensure the partitions contain activity labels with similar proportions.

% Extract predictors and response
predictors = featureTable(:, 1:end-1);
response = featureTable.ActivityID;

% For reproducible results
rng default

% Partition the data and extract training predictors and response data
cvp = cvpartition(response,'Holdout',0.25);
trainingPredictors = predictors(cvp.training, :);
trainingResponse = response(cvp.training, :);

% Train the classifier
template = templateSVM(...
    'KernelFunction', 'polynomial', ...
    'PolynomialOrder', 2, ...
    'KernelScale', 'auto', ...
    'BoxConstraint', 1, ...
    'Standardize', true);
classificationSVM = fitcecoc(...
    trainingPredictors, ...
    trainingResponse, ...
    'Learners', template, ...
    'Coding', 'onevsone', ...
    'ClassNames',actioncats);

Test the classifier on the test partition and analyze its classification accuracy.

% Extract test predictors and response data
testPredictors = predictors(cvp.test, :);
testResponse = response(cvp.test, :);

% Predict activity on the test data
testPredictions = predict(classificationSVM,testPredictors);

% Plot the confusion matrix to analyze performance of the classifier
figure
cm = confusionchart(testResponse, testPredictions, ...
    ColumnSummary="column-normalized", RowSummary="row-normalized");

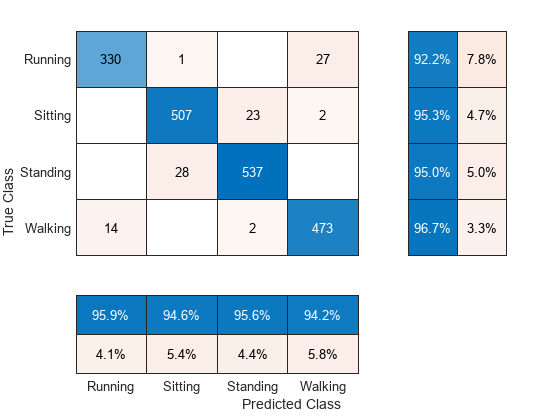
accuracy = trace(cm.NormalizedValues)/sum(cm.NormalizedValues, "all");
fprintf("The classification accuracy on the test partition is %2.1f%%", accuracy*100)

The classification accuracy on the test partition is 95.0%

Most of the errors occur when misclassifying running as walking and standing as sitting.

Summary

In this example, you saw how to extract features for human activity based on smartphone sensor signals using signalTimeFeatureExtractor and signalFrequencyFeatureExtractor. You saw how to use the extracted features to train an SVM model which resulted in about 95% accuracy. As an alternative approach, you can also explore using a featureInput layer to train a deep learning classifier.

References

[1] El Helou, A. Sensor HAR recognition App. MathWorks File Exchange https://www.mathworks.com/matlabcentral/fileexchange/54138-sensor-har-recognition-app

[2] El Helou, A. Sensor Data Analytics. MathWorks File Exchange https://www.mathworks.com/matlabcentral/fileexchange/54139-sensor-data-analytics-french-webinar-code