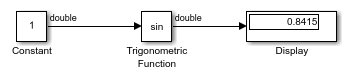
Trigonometric Function

指定应用于输入信号的三角函数

库:
Simulink / Math Operations
HDL Coder / Math Operations
HDL Coder / HDL Floating Point Operations

描述

Trigonometric Function 模块执行常见的三角函数，并以 rad 或 rev 为单位输出结果。

支持的函数

可以从函数下拉列表中选择以下函数之一。

函数	描述	数学表达式	MATLAB^® 等效函数
`sin`	输入信号的正弦	`sin(u)`	`sin`
`cos`	输入信号的余弦	`cos(u)`	`cos`
`tan`	输入信号的正切	`tan(u)`	`tan`
`asin`	输入信号的反正弦	`asin(u)`	`asin`
`acos`	输入信号的反余弦	`acos(u)`	`acos`
`atan`	输入信号的反正切	`atan(u)`	`atan`
`atan2`	输入信号的四象限反正切	`atan2(u)`	`atan2`
`sinh`	输入信号的双曲正弦	`sinh(u)`	`sinh`
`cosh`	输入信号的双曲余弦	`cosh(u)`	`cosh`
`tanh`	输入信号的双曲正切	`tanh(u)`	`tanh`
`asinh`	输入信号的反双曲正弦	`asinh(u)`	`asinh`
`acosh`	输入信号的反双曲余弦	`acosh(u)`	`acosh`
`atanh`	输入信号的反双曲正切	`atanh(u)`	`atanh`
`sincos`	输入信号的正弦；输入信号的余弦	—	—
`cos + jsin`	输入信号的复指数	—	—

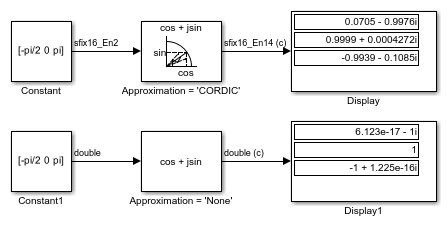
CORDIC 逼近方法

CORDIC 是 COordinate Rotation DIgital Computer（坐标旋转数字计算方法）的缩写。基于吉文斯旋转的 CORDIC 算法是最节省硬件资源的可用算法之一，因为它只需进行迭代移位相加运算。有关详细信息，请参阅详细信息。模块输入有进一步的要求。

有关何时将函数设置为 sin、cos、sincos 或 cos + jsin，并将逼近方法设置为 CORDIC 的详细信息，请参阅 Port_1。

下表概述了输入无效时发生的情况。

模块用法	无效输入的影响
仿真模式	出现错误。
生成的代码	发生未定义的行为。对于生成的代码，避免依赖未定义的行为。

查找逼近方法

有关何时将函数设置为 sin、cos、sincos 或 cos + jsin，并将逼近方法设置为查找的详细信息，请参阅 Port_1。

示例

全部展开

具有浮点输入的 sin 函数

打开模型

此示例说明如何使用 Trigonometric Function 模块来计算浮点输入的正弦值。Trigonometric Function 模块的输出的数据类型与输入的数据类型相同，因为输入数据类型为浮点类型，逼近方法为 none。

具有定点输入的 sincos 函数

此示例使用:

打开模型

此示例说明如何使用 Trigonometric Function 模块计算定点输入信号的 sincos 的 CORDIC 逼近。

Trigonometric Function 模块参数如下：

函数：sincos
逼近方法：CORDIC
迭代次数：11

使用 CORDIC 逼近方法时，Trigonometric Function 模块的输入必须在范围 [-2pi,2pi) 内。Trigonometric Function 模块的输出类型为 fixdt(1,13,11)，因为输入是定点信号且逼近方法设置为 CORDIC。输出小数长度等于输入字长减二。

复指数输出的 Trigonometric Function 模块行为

此示例使用:

打开模型

此示例比较 Trigonometric Function 模块的两种不同配置的复指数输出。

当逼近方法为 CORDIC 时，输入数据类型可以是定点，在本例中为 fixdt(1,16,2)。输出数据类型为 fixdt(1,16,14)，因为输出小数长度等于输入字长减二。

当逼近方法为 None 时，输入数据类型必须为浮点类型。输出数据类型与输入数据类型相同。

限制

仅当逼近方法设置为 CORDIC 或查找时，才可以使用定点输入信号。CORDIC 和查找逼近可用于 sin、cos、sincos、cos + jsin 和 atan2 函数。
除 atan2 之外，此模块中的所有函数都支持复输入信号。
当您将逼近方法设置为查找时，数据点的数量受到以下因素的限制：
- smallEnoughNumDataPoints = 2^{(inputFractionLen-2)}+1
- bigEnoughFractionLen = log2(numberOfDataPoints - 1)+2
其中：
- smallEnoughNumDataPoints 是由指定的输入小数长度 inputFractionLen 表示的最大数据点数。
- bigEnoughFractionLen 是表示指定的数据点数 numberOfDataPoints 所需的最小小数长度。
当您将函数设置为 sin、cos、sincos 或 cos + jsin 并将逼近方法设置为 CORDIC 时，模块具有以下限制：
- 当您使用有符号定点类型时，输入角必须在 [–2π, 2π) 弧度范围内。
- 当您使用无符号定点类型时，输入角必须在 [0, 2π) 弧度范围内。
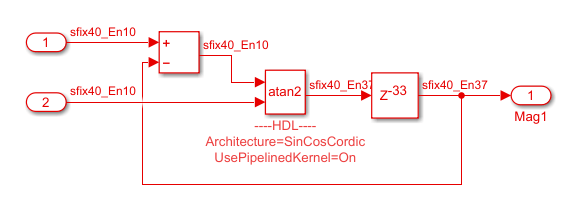
当您将函数设置为 atan2 且逼近方法设置为 CORDIC 时，模块具有以下限制：
- 输入的大小必须相同，或者至少一个值必须是标量值。
- 两个输入必须具有相同的数据类型。
- 当您使用有符号定点类型时，字长必须等于或小于 126。
- 当您使用无符号定点类型时，字长必须等于或小于 125。
当您将函数设置为 sin、cos、sincos 或 cos + jsin 并将逼近方法设置为查找时，模块具有以下限制。
- 当您使用有符号定点类型时，输入角必须在 [-2π,2π] 弧度范围内。
- 当您使用无符号定点类型时，输入角必须在 [0,2π) 弧度范围内。
当您将函数设置为 atan2 且逼近方法设置为查找时，模块具有以下限制：
- 输入的大小必须相同，或者至少一个值必须是标量值。
- 两个输入必须具有相同的数据类型。

端口

输入

全部展开

Port_1 — 输入信号
标量 | 向量 | 矩阵

指定为标量、向量或矩阵的输入。此模块接受以下数据类型的输入信号：

函数	输入数据类型
`sin` `cos` `sincos` `cos + jsin` `atan2`	浮点定点（仅当逼近方法为 CORDIC 或查找时）
`tan` `asin` `acos` `atan` `sinh` `cosh` `tanh` `asinh` `acosh` `atanh`	浮点

CORDIC 逼近定点类型传播：

输入数据类型函数输出数据类型

输入数据类型	函数	输出数据类型
定点，有符号或无符号	`sin`、`cos`、`sincos` 和 `cos + jsin`	`fixdt(1, WL, WL - 2)`，其中 `WL` 是输入的字长此定点类型为 CORDIC 算法提供最佳精度。
定点，有符号	`atan2`	`fixdt(1, WL, WL – 3)`
定点，无符号	`atan2`	`fixdt(1, WL, WL – 2)`

定点，有符号或无符号

sin、cos、sincos 和 cos + jsin

fixdt(1, WL, WL - 2)，其中 WL 是输入的字长

此定点类型为 CORDIC 算法提供最佳精度。

定点，有符号

atan2

fixdt(1, WL, WL – 3)

定点，无符号

atan2

fixdt(1, WL, WL – 2)

查找逼近定点类型传播：

输入数据类型	函数	输出数据类型
定点，有符号	`sin`, `cos`, `sincos`, `cos + jsin`, `atan2`	`fixdt(1, WL, FL)`
定点，无符号	`sin`, `cos`, `sincos`, `cos + jsin`, `atan2`	`fixdt(1, WL - 1, FL)`

依赖关系

当您将函数设置为 atan2 时，模块显示两个输入端口。第一个输入 (Port_1) 是函数参量的 y 轴坐标，即虚部。第二个输入 (Port_2) 是函数参量的 x 轴坐标，即实部。

如果您将逼近方法设置为无、CORDIC 或查找，则可以使用浮点输入信号。但是，模块输出的数据类型取决于您选择的逼近方法选项。

输入数据类型	逼近方法	输出数据类型
浮点	无	取决于您选择的输出信号类型。选项为 `auto`（与输入的数据类型相同）、`real` 或 `complex`。
浮点	CORDIC	与输入相同。当您使用 CORDIC 逼近方法计算模块输出时，输出信号类型不可用。
浮点	查找	与输入相同。当您使用 Lookup 逼近方法计算模块输出时，输出信号类型不可用。

对于 CORDIC 和查找逼近：

sin、cos、sincos、cos + jsin 和 atan2 函数的输入必须是实数。
sin、cos、sincos 和 atan2 函数的输出为实数。
cos + jsin 函数的输出为复数。

有关详细信息，请参阅限制。

Port_2 — `atan2` 的函数参量的 x 轴坐标，即实部
标量 | 向量 | 矩阵

输入 atan2 的函数参量的 x 轴坐标，即实部。当您将函数设置为 atan2 时，模块显示两个输入端口。第一个输入 (Port_1) 是函数参量的 y 轴坐标，即虚部。第二个输入 (Port_2) 是函数参量的 x 轴坐标，即实部。（有关各种模块方向的端口顺序的描述，请参阅标识旋转或翻转模块上的端口位置。）

仅当逼近方法设置为 CORDIC 或查找时才支持定点输入信号。

依赖关系

要启用此端口，请将函数设置为 atan2。

输出

全部展开

Port_1 — 指定输入信号的三角函数
标量 | 向量 | 矩阵

将指定的三角函数应用于一个或多个输入（以 rad 为单位）的结果。每个函数支持：

标量运算
按元素的向量和矩阵运算

sin — 输入信号的正弦
标量 | 向量 | 矩阵

输入信号的正弦，以 rad 和 rev 为单位。

依赖关系

要启用此端口，请将函数设置为 sincos。

cos — 输入信号的余弦
标量 | 向量 | 矩阵

输入信号的余弦，以 rad 和 rev 为单位。

依赖关系

要启用此端口，请将函数设置为 sincos。

参数

全部展开

算法

函数 — 三角函数
sin (默认) | cos | tan | asin | acos | atan | atan2 | sinh | cosh | Tanh | asinh | acosh | atanh | sincos | cos + jsin

指定三角函数。模块图标上的函数名称发生变化以反映您的选择。

有关何时将函数设置为 sin、cos、sincos 或 cos + jsin，并将逼近方法设置为 CORDIC 的详细信息，请参阅限制。

编程用法

模块参数：Operator

类型：字符向量

值：

'sin' | 'cos' | 'tan' | 'asin' | 'acos' | 'atan' | 'atan2' | 'sinh' | 'cosh' | 'tanh' | 'asinh' | 'acosh' | 'atanh' | 'sincos' | 'cos + jsin'

默认值：'sin'

逼近方法 — CORDIC、查找或无
无 (默认) | CORDIC | 查找

指定计算输出的逼近方法类型。

逼近方法	支持的数据类型	何时使用此方法
无（默认值）	浮点	您想使用默认的泰勒级数算法。
CORDIC	浮点和定点	您需要快速的近似迭代计算。
查找	浮点（双精度和单精度）和定点，其偏置值为 `0`，斜率值为 2 的幂	您需要快速的近似查找表实现。

有关何时将函数设置为 sin、cos、sincos 或 cos + jsin，并将逼近方法设置为 CORDIC 的详细信息，请参阅限制。

依赖关系

要启用此参数，请将函数设置为 sin、cos、sincos、cos + jsin 或 atan2。
要使用定点输入信号，必须将逼近方法设置为 CORDIC 或查找。
要启用表数据类型参数，请将此方法设置为查找。

编程用法

模块参数：ApproximationMethod

类型：字符向量

值：'None' | 'CORDIC' | 'Lookup'

默认值：'None'

插值方法 — 断点值之间插值的方法
线性点-斜率 (默认) | 均一

当输入位于两个断点值之间时，模块将根据相邻断点内插输出值。有关插值方法的详细信息，请参阅内插方法。

编程用法

模块参数：InterpMethod

类型：字符向量

值：'Linear point-slope' | 'Flat'

默认值：'Linear point-slope'

迭代次数 — CORDIC 算法的迭代次数
`11` (默认) | 正整数，小于或等于定点输入的字长

指定要执行 CORDIC 算法的迭代次数。默认值为 11。

当模块输入使用浮点数据类型时，迭代次数可以是正整数。
当模块输入是定点数据类型时，迭代次数不能超过字长。
例如，如果模块输入是 fixdt(1,16,15)，字长为 16。在这种情况下，迭代次数不能超过 16。

依赖关系

要启用此参数，必须按如下所示设置函数和逼近方法参数：

将函数设置为 sin、cos、sincos、cos + jsin 或 atan2。
将逼近方法设置为 CORDIC。

编程用法

模块参数：NumberOfIterations

类型：字符向量

值：正整数，小于等于定点输入的字长

默认值：'11'

角度单位 — 角度单位
radian (默认) | revolution

将查找方法的角度单位指定为 radian 或 revolution。

依赖关系

要启用此参数，请进行如下设置：

将函数设置为 sin、cos、sincos、cos + jsin 或 atan2。
将逼近方法设置为查找。

编程用法

模块参数：AngleUnit

类型：字符向量

值：'radian' | 'revolution'

默认值：'radian'

数据点数 — 查找表的数据点数
`16` (默认) | 标量

将查找表的数据点数指定为标量实数。

依赖关系

要启用此参数，请进行如下设置：

将函数设置为 sin、cos、sincos、cos + jsin 或 atan2。
将逼近方法设置为查找。

编程用法

模块参数：NumberOfDataPoints

类型：字符向量

值：标量

默认值：'16'

输出信号类型 — 输出信号的复/实性
自动 (默认) | 实数 | 复

将 Trigonometric Function 模块输出信号类型指定为 auto、real 或 complex。

函数	输入信号类型	输出信号类型
函数	输入信号类型	自动	实数	复数
任意函数参数选择项	实数	实数	实数	复数
任意函数参数选择项	复数	复数	错误	复数

依赖关系

将逼近方法设置为 CORDIC 将禁用此参数。

注意

当函数为 atan2 时，仿真或代码生成不支持复输入信号。

编程用法

模块参数：OutputSignalType

类型：字符向量

值：'auto' | 'real' | 'complex'

默认值：'auto'

删除防止超范围输入的代码 — 删除防止超范围输入的代码
off (默认) | on

对于 acos 和 asin，选中此复选框将不会防范超出范围的输入，从而减少冗余。

如果清除此复选框，则会启用防范。在执行任何操作之前，模块会将超出范围的输入饱和处理为 1 或 -1。生成的代码包含用于检查超出范围输入的代码。
如果选中此复选框，则会取消防范。模块将对输入值执行所有运算而不进行任何更改。生成的代码不包含用于检查超出范围输入的代码。

如果输入已在范围内，启用此复选框可以消除冗余。

依赖关系

将函数设置为 acos 和 asin 会启用此参数。

编程用法

模块参数：RemoveProtectionAgainstOutOfRangeInput

类型：字符向量

值：'off' | 'on'

默认值：'off'

采样时间(-1 表示继承) — 采样之间的时间间隔
`-1` (默认) | 标量 | 向量

指定采样时间间隔。要继承采样时间，请将此参数设置为 -1。有关详细信息，请参阅指定采样时间。

依赖关系

仅当您将此参数设置为 -1 以外的值时才可见。要了解详细信息，请参阅不建议设置采样时间的模块。

编程用法

要以编程方式设置模块参数值，请使用 set_param 函数。

参数:	`SampleTime`
值:	`"-1"` (默认) \| scalar or vector in quotes

数据类型

表数据类型 — 表的数据类型
继承: 从输入继承 (默认) | double | single | fixdt(1,16,0) | <数据类型表达式>

查找表的数据类型，指定为：

继承: 从输入继承
double
single
fixdt(1,16,0)
<数据类型表达式>

有关设置数据类型的详细信息，请参阅控制信号的数据类型。

编程用法

模块参数：TableDataTypeStr

类型：字符串标量或字符向量

值： Inherit: Inherit via input | single | double | fixdt(1,16,0) | 数据类型表达式

默认值：Inherit: Inherit via input

模式 — 要指定的数据的类别
继承 (默认) | 内置 | 定点 | 表达式

选择您要如何指定输出数据类型的数据类型属性。您可以选择：

继承 - 用于指定继承数据类型的规则，例如继承: 从内部规则继承
内置 - 用于指定内置数据类型。
定点 - 用于指定数据类型的定点属性。
表达式 - 用于指定计算结果为有效数据类型的表达式，例如 fixdt([],16,0)

依赖关系

要启用此参数，请在输出数据类型参数处点击 >>。

符号性 — 指定有符号或无符号
`Signed` (默认) | `Unsigned`

为输出数据类型指定符号性。

依赖关系

要启用此参数，请将模式设置为定点。

定标 — 定标定点数据的方法
二进制小数点 (默认)

为输出数据类型指定定标。

依赖关系

要启用此参数，请将模式设置为定点。

数据类型覆盖 — 为此信号指定数据类型覆盖模式
`Inherit` | `Off`

为此信号选择数据类型覆盖模式。

继承 - 继承为模型指定的数据类型覆盖设置。
关闭 - 忽略为模型指定的数据类型覆盖设置，并使用您指定的定点数据类型

有关详细信息，请参阅 Simulink^® 文档中的使用数据类型助手指定数据类型。

提示

由于能够关闭单个数据类型的数据类型覆盖，您可以在应用数据类型覆盖时更好地控制模型中的数据类型。例如，您可以使用此选项确保数据类型满足下游模块的要求，而忽略数据类型覆盖设置。

依赖关系

要启用此参数，请点击显示数据类型助手按钮，并将模式设置为内置或定点。

字长 — 存储量化整数的字的位大小
`16` (默认) | 从 0 到 32 的整数

指定存储量化整数的字的位大小。有关详细信息，请参阅指定定点数据类型。

依赖关系

要启用此参数，请将模式设置为定点。

小数长度 — 指定定点数据类型的小数长度
`0` (默认) | 整数标量

将定点数据类型的小数长度指定为正整数或负整数。有关详细信息，请参阅指定定点数据类型。

依赖关系

要启用此参数，请进行如下设置：

将模式设置为定点
将定标设置为二进制小数点

模块特性

数据类型	`double` \| `fixed point^a` \| `half` \| `integer^a` \| `single`
直接馈通	`是`
多维信号	`是`
可变大小信号	`是`
过零检测	`否`
^a 当采用 CORDIC 逼近方法时，此模块支持定点和基整数数据类型。

详细信息

全部展开

CORDIC

CORDIC 是 Coordinate Rotation DIgital Computer（坐标旋转数字计算方法）的缩写。基于吉文斯旋转的 CORDIC 算法是最节省硬件资源的可用算法之一，因为它只需进行迭代移位相加运算（请参阅“参考资料”）。CORDIC 算法不需要显式乘数。使用 CORDIC，您可以计算各种函数，如正弦、余弦、反正弦、反余弦、反正切和向量幅值。您可以将此算法用于除法、平方根、双曲线和对数函数。

增加 CORDIC 迭代次数可以得出更准确的结果，但这样会增加计算开销和延迟。

参考

[1] Volder, Jack E., “The CORDIC Trigonometric Computing Technique.” IRE Transactions on Electronic Computers EC-8 (1959); 330–334.

[2] Andraka, Ray “A Survey of CORDIC Algorithm for FPGA Based Computers.” Proceedings of the 1998 ACM/SIGDA Sixth International Symposium on Field Programmable Gate Arrays. Feb. 22–24 (1998): 191–200.

[3] Walther, J.S., “A Unified Algorithm for Elementary Functions,” Proceedings of the Spring Joint Computer Conference, May 18-20, 1971: 379–386.

[4] Schelin, Charles W., “Calculator Function Approximation,” The American Mathematical Monthly 90, no. 5 (1983): 317–325.

扩展功能

全部展开

C/C++ 代码生成
使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。

并非所有编译器都支持 asinh、acosh 和 atanh 函数。如果您使用不支持这些函数的编译器，将会出现警告，且生成的代码无法链接。

HDL 代码生成
使用 HDL Coder™ 为 FPGA 和 ASIC 设计生成 VHDL、Verilog 和 SystemVerilog 代码。

HDL Coder™ 提供影响 HDL 实现和综合逻辑的额外配置选项。

HDL 架构

要从使用定点数据的模块中生成 HDL 代码，请将架构设置为 Cordic 或 LUT。下表显示模块支持这些设置的函数：

模块参数	HDL 模块属性	支持的函数
将逼近方法设置为 CORDIC，将数据点数设置为任何标量实数。	将架构设置为 Cordic。	sin cos sincos cos+jsin atan2
将逼近方法设置为查找，将插值方法设置为均一，将角度单位设置为转，将数据点数设置为任何标量实数。	将架构设置为 LUT。	sin cos sincos cos+jsin

要为使用浮点数据的模块的所有函数生成 HDL 代码，请将逼近方法模块参数设置为无，并将输出信号类型参数设置为自动或实数或复数。此外，将 HDL 模块属性中的架构参数设置为三角函数。

此模块具有多周期实现，这会在生成的代码中引入额外的延迟。要查看增加的延迟，请查看生成的模型或验证模型。请参阅Generated Model and Validation Model (HDL Coder)。

延迟计算取决于字长和 LatencyStrategy 设置。要查看定点数据类型的延迟计算，请参阅：

Sin (HDL Coder)
Cos (HDL Coder)
Cos+jSin (HDL Coder)
SinCos (HDL Coder)
Atan2 (HDL Coder)

HDL 模块属性

通用
ConstrainedOutputPipeline	通过移动设计中现有延迟的方式来放置在输出端的寄存器的数量。分布式流水线不会重新分发这些寄存器。默认值为 `0`。有关详细信息，请参阅ConstrainedOutputPipeline (HDL Coder)。
InputPipeline	要在生成的代码中插入的输入流水线阶段数。分布式流水线和受限输出流水线可以移动这些寄存器。默认值为 `0`。有关详细信息，请参阅InputPipeline (HDL Coder)。
OutputPipeline	要在生成的代码中插入的输出流水线阶段数。分布式流水线和受限输出流水线可以移动这些寄存器。默认值为 `0`。有关详细信息，请参阅OutputPipeline (HDL Coder)。
LatencyStrategy	要为定点类型启用此属性，请将函数设置为 `sin`、`cos`、`sincos`、`cos+jsin`，或 `atan2` 并将逼近方法设置为 `CORDIC`。对于定点和浮点类型，指定是将设计中的模块映射到 `MAX`、`Min`、`CUSTOM` 还是 `ZERO` 延迟。默认值为 MAX。另请参阅LatencyStrategy (HDL Coder)。
CustomLatency	要为定点类型启用此属性，请将函数设置为 `sin`、`cos`、`sincos`、`cos+jsin`，或 `atan2` 并将逼近方法设置为 `CORDIC`。当 LatencyStrategy 设置为 `CUSTOM` 时，使用此属性为定点类型指定介于 `ZERO` 和 `MAX` 之间的自定义延迟值。另请参阅LatencyStrategy (HDL Coder)。
IterationsPerPipeline	要为定点类型启用此属性，请将函数设置为 `sin`、`cos`、`sincos`、`cos+jsin`，或 `atan2` 并将逼近方法设置为 `CORDIC`。当 LatencyStrategy 设置为 `Custom(PerIterations)` 时，使用此设置指定每个流水线阶段的迭代次数。有关详细信息，请参阅Atan2 (HDL Coder)。

原生浮点
InputRangeReduction	将此属性用于 `sin`、`cos`、`sincos`、`cos+jsin` 和 `atan2` 函数。如果您的输入范围是无界的，请为 HDL Coder 启用此属性，以插入额外的逻辑来缩小 `[-pi, pi]` 的输入范围。另请参阅InputRangeReduction (HDL Coder)。
HandleDenormals	指定是否希望 HDL Coder 在设计中插入额外的逻辑来处理非正规数字。非正规数是大小非常小、必须使用包含前导零的尾数才能表示的浮点数。默认值为 inherit。另请参阅HandleDenormals (HDL Coder)。
LatencyStrategy	指定对于浮点运算符是否将设计中的模块映射到 `inherit`、`Max`、`Min` 或 `Zero`。默认值为 inherit。另请参阅LatencyStrategy (HDL Coder)。
MultiplyStrategy	将此属性用于 `sin`、`cos`、`sincos`、`cos+jsin` 和 `atan2` 函数。默认值为 `inherit`。指定您要使用 `FullMultiplier` 还是 `PartMultiplierPartAddShift`。另请参阅MantissaMultiplyStrategy (HDL Coder)。

ULP 注意事项

对于浮点运算，Trigonometric Function 模块的最后一位非零单位 (ULP) 误差。有关详细信息，请参阅ULP Considerations of Native Floating-Point Operators (HDL Coder)。

限制

对于 sin 和 cos 函数，该模块仅支持将有符号定点数据类型用于 CORDIC 逼近。
对于具有 CORDIC 模式的函数，如 sin、cos、sincos、atan2 和 cos+jsin，HDL 代码生成不支持大于 127 位的定点数据类型。
HDL 代码生成不支持对三角函数使用双精度数据类型，但 sin 和 cos 函数除外。
在以下情况下，HDL 代码生成不支持查找逼近方法：
- 插值方法参数设置为线性点-斜率，角度单位参数设置为弧度或旋转。
- 插值方法参数为均一，角度单位参数为弧度。
当 Trigonometric Function 模块位于反馈环中且采用以下设置时，HDL Coder 会显示错误：
- 将架构设置为 Cordic
- 将 UsePipelinedKernel 设置为 On
出现错误是因为该模块处于反馈环中，并且代码生成器无法插入额外的延迟。为避免此错误，请在模块附近添加长度等于迭代次数 + 3 的延迟。然后，代码生成器吸收该延迟以满足 Trigonometric Function 模块的额外延迟。
例如，此 Trigonometric Function 模块将迭代次数设置为 30。添加与该模块相邻的长度为 33 的 Delay 模块满足额外的延迟。

PLC 代码生成
使用 Simulink® PLC Coder™ 生成结构化文本代码。

定点转换
使用 Fixed-Point Designer™ 设计和仿真定点系统。

当函数设置为 sin、cos、sincos、cos + jsin 或 atan2 且逼近方法设置为 CORDIC 时，此模块支持定点和基整数数据类型。

版本历史记录

在 R2006a 之前推出

另请参阅

模块

Math Function | Sqrt | Sine, Cosine

函数

cordicsin (Fixed-Point Designer) | cordiccos (Fixed-Point Designer) | cordicsincos (Fixed-Point Designer)

Trigonometric Function

描述

支持的函数

CORDIC 逼近方法

查找逼近方法

示例

具有浮点输入的 sin 函数

具有定点输入的 sincos 函数

复指数输出的 Trigonometric Function 模块行为

限制

端口

输入

Port_1 — 输入信号 标量 | 向量 | 矩阵

依赖关系

Port_2 — atan2 的函数参量的 x 轴坐标，即实部 标量 | 向量 | 矩阵

依赖关系

输出

Port_1 — 指定输入信号的三角函数 标量 | 向量 | 矩阵

sin — 输入信号的正弦 标量 | 向量 | 矩阵

依赖关系

cos — 输入信号的余弦 标量 | 向量 | 矩阵

依赖关系

参数

算法

函数 — 三角函数 sin (默认) | cos | tan | asin | acos | atan | atan2 | sinh | cosh | Tanh | asinh | acosh | atanh | sincos | cos + jsin

编程用法

逼近方法 — CORDIC、查找或无 无 (默认) | CORDIC | 查找

依赖关系

编程用法

插值方法 — 断点值之间插值的方法 线性点-斜率 (默认) | 均一

编程用法

迭代次数 — CORDIC 算法的迭代次数 11 (默认) | 正整数，小于或等于定点输入的字长

依赖关系

编程用法

角度单位 — 角度单位 radian (默认) | revolution

依赖关系

编程用法

数据点数 — 查找表的数据点数 16 (默认) | 标量

依赖关系

编程用法

输出信号类型 — 输出信号的复/实性 自动 (默认) | 实数 | 复

依赖关系

编程用法

删除防止超范围输入的代码 — 删除防止超范围输入的代码 off (默认) | on

依赖关系

编程用法

采样时间(-1 表示继承) — 采样之间的时间间隔 -1 (默认) | 标量 | 向量

依赖关系

编程用法

数据类型

表数据类型 — 表的数据类型 继承: 从输入继承 (默认) | double | single | fixdt(1,16,0) | <数据类型表达式>

编程用法

模式 — 要指定的数据的类别 继承 (默认) | 内置 | 定点 | 表达式

依赖关系

符号性 — 指定有符号或无符号 Signed (默认) | Unsigned

依赖关系

定标 — 定标定点数据的方法 二进制小数点 (默认)

依赖关系

数据类型覆盖 — 为此信号指定数据类型覆盖模式 Inherit | Off

提示

依赖关系

字长 — 存储量化整数的字的位大小 16 (默认) | 从 0 到 32 的整数

依赖关系

小数长度 — 指定定点数据类型的小数长度 0 (默认) | 整数标量

依赖关系

模块特性

详细信息

CORDIC

参考

扩展功能

C/C++ 代码生成 使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。

HDL 代码生成 使用 HDL Coder™ 为 FPGA 和 ASIC 设计生成 VHDL、Verilog 和 SystemVerilog 代码。

PLC 代码生成 使用 Simulink® PLC Coder™ 生成结构化文本代码。

定点转换 使用 Fixed-Point Designer™ 设计和仿真定点系统。

版本历史记录

另请参阅

模块

函数

Port_1 — 输入信号
标量 | 向量 | 矩阵

Port_2 — `atan2` 的函数参量的 x 轴坐标，即实部
标量 | 向量 | 矩阵

Port_1 — 指定输入信号的三角函数
标量 | 向量 | 矩阵

sin — 输入信号的正弦
标量 | 向量 | 矩阵

cos — 输入信号的余弦
标量 | 向量 | 矩阵

函数 — 三角函数
sin (默认) | cos | tan | asin | acos | atan | atan2 | sinh | cosh | Tanh | asinh | acosh | atanh | sincos | cos + jsin

逼近方法 — CORDIC、查找或无
无 (默认) | CORDIC | 查找

插值方法 — 断点值之间插值的方法
线性点-斜率 (默认) | 均一

迭代次数 — CORDIC 算法的迭代次数
`11` (默认) | 正整数，小于或等于定点输入的字长

角度单位 — 角度单位
radian (默认) | revolution

数据点数 — 查找表的数据点数
`16` (默认) | 标量

输出信号类型 — 输出信号的复/实性
自动 (默认) | 实数 | 复

删除防止超范围输入的代码 — 删除防止超范围输入的代码
off (默认) | on

采样时间(-1 表示继承) — 采样之间的时间间隔
`-1` (默认) | 标量 | 向量

表数据类型 — 表的数据类型
继承: 从输入继承 (默认) | double | single | fixdt(1,16,0) | <数据类型表达式>

模式 — 要指定的数据的类别
继承 (默认) | 内置 | 定点 | 表达式

符号性 — 指定有符号或无符号
`Signed` (默认) | `Unsigned`

定标 — 定标定点数据的方法
二进制小数点 (默认)

数据类型覆盖 — 为此信号指定数据类型覆盖模式
`Inherit` | `Off`

字长 — 存储量化整数的字的位大小
`16` (默认) | 从 0 到 32 的整数

小数长度 — 指定定点数据类型的小数长度
`0` (默认) | 整数标量

C/C++ 代码生成
使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。

HDL 代码生成
使用 HDL Coder™ 为 FPGA 和 ASIC 设计生成 VHDL、Verilog 和 SystemVerilog 代码。

PLC 代码生成
使用 Simulink® PLC Coder™ 生成结构化文本代码。

定点转换
使用 Fixed-Point Designer™ 设计和仿真定点系统。