Main Content

estimateCameraProjection

Estimate camera projection matrix from world-to-image point correspondences

Since R2022b

collapse all in page

Syntax

camProjection = estimateCameraProjection(imagePoints,worldPoints)
[camProjection,reprojectionErrors] = estimateCameraProjection(imagePoints,worldPoints)

Description

camProjection = estimateCameraProjection(imagePoints,worldPoints) returns the camera projection matrix determined from known world points and their corresponding image projections by using the direct linear transformation (DLT) approach.

[camProjection,reprojectionErrors] = estimateCameraProjection(imagePoints,worldPoints) also returns the reprojection error that quantifies the accuracy of the projected image coordinates.

example

Examples

collapse all

Open Live Script

Load a 3-D point cloud data captured by an RGB-D sensor into the workspace.

load("object3d.mat");

Remove points with Inf or NaN coordinates from the point cloud.

[validPtCloud,validIndices] = removeInvalidPoints(ptCloud);

Read the valid world point coordinates. Each entry specifies the (x, y, z) coordinates of a point in the point cloud.

worldPoints = validPtCloud.Location;

Define the corresponding image point coordinates as an orthographic projection of point cloud data onto the yz-plane.

indices = 1:ptCloud.Count;
[y,z] = ind2sub([size(ptCloud.Location,1),size(ptCloud.Location,2)],indices);
imagePoints = [y(validIndices)' z(validIndices)'];

Generate the 2-D image projection by using the image point coordinates and their color values.

projImage = zeros(max(imagePoints(:,1)),max(imagePoints(:,2)),3);
rgb = validPtCloud.Color;
for j = 1:length(rgb)
    projImage(imagePoints(j,1),imagePoints(j,2),:) = rgb(j,:);
end

Display the point cloud data and the corresponding 2-D image projection.

figure
subplot(1,2,1)
pcshow(ptCloud)
xlabel("X");
ylabel("Y");
zlabel("Z");
title("Point Cloud Data",Color=[1 1 1])
subplot(1,2,2)
imshow(uint8(projImage))
title("2-D Image Projection",Color=[1 1 1])

Figure contains 2 axes objects. Axes object 1 with title Point Cloud Data, xlabel X, ylabel Y contains an object of type scatter. Hidden axes object 2 with title 2-D Image Projection contains an object of type image.

Estimate the camera projection matrix and reprojection error by using the known world points and the image points.

[camProjection,reprojectionErrors] = estimateCameraProjection(imagePoints,worldPoints);

Use the estimated camera projection matrix as input to the findNearestNeighbors function and find the nearest neighbors of a query point.

point = [0.4 0.3 0.2]; 
K = 50;    % Specify the number of nearest neighbors to be determined
[indices,dists] = findNearestNeighbors(ptCloud,point,K,camProjection');

Use the select function to get the point cloud data of nearest neighbors.

ptCloudB = select(ptCloud,indices);

Display the input point cloud and its nearest neighbors.

figure
pcshow(ptCloud)
hold on
plot3(ptCloudB.Location(:,1),ptCloudB.Location(:,2),ptCloudB.Location(:,3),"*")
hold off
legend("Point Cloud","Nearest Neighbors",Location="southoutside",Color=[1 1 1])

Figure contains an axes object. The axes object contains 2 objects of type scatter, line. One or more of the lines displays its values using only markers These objects represent Point Cloud, Nearest Neighbors.

Input Arguments

collapse all

Coordinates of image projection points, specified as an M-by-2 matrix of (x, y) coordinates. M is the number of points and it must be greater than or equal to 6. The input image points must correspond to an undistorted image plane.

Data Types: single | double

3-D world points, specified as an M-by-3 matrix of non-coplanar (x, y, z) coordinates. M is the number of points and must be greater than or equal to 6.

Data Types: single | double

Output Arguments

collapse all

Camera projection matrix, returned as a 3-by-4 matrix. The matrix maps the 3-D world points, in homogenous coordinates, to the 2-D image coordinates of the projections onto the image plane.

Using the camera projection matrix and homogeneous coordinates, you can project a world point onto the image.

w × [x,y,1]' = camProjection× [X,Y,Z,1]'

(X,Y,Z) are the world coordinates of a point
(x,y) are the coordinates of the corresponding image point
w is an arbitrary scale factor

Data Types: double

Reprojection errors, returned as a M-by-1 vector. The reprojection error is the error between the reprojected image points and the input image points. For more information on the computation of reprojection errors, see Algorithms.

Data Types: double

Tips

  • This function assumes the camera has negligible lens distortion. If there is lens distortion, calibrate the camera and use the estworldpose and cameraProjection functions instead.

  • If the camera intrinsics and extrinsics parameters are known, you can estimate the camera projection matrix using the cameraProjection function.

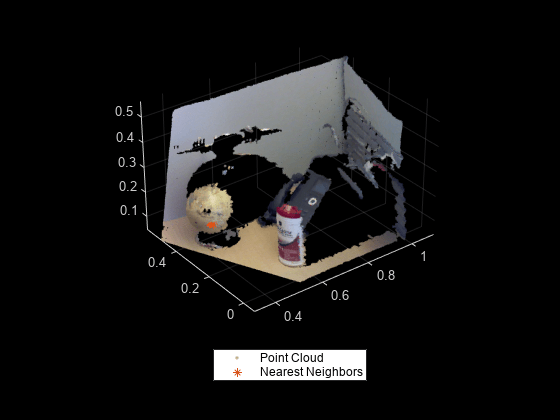
  • You can use the camera projection matrix, camProjection, with the findNearestNeighbors function to speed up the nearest neighbors search in a point cloud generated by an RGB-D sensor, such as Microsoft® Kinect®.

Algorithms

Given the world points X and the image points x, the camera projection matrix C, is obtained by solving the equation

λx = CX.

The equation is solved using the direct linear transformation (DLT) approach [1]. This approach formulates a homogeneous linear system of equations, and the solution is obtained through generalized eigenvalue decomposition.

Because the image point coordinates are given in pixel values, the approach for computing the camera projection matrix is sensitive to numerical errors. To avoid numerical errors, the input image point coordinates are normalized, so that their centroid is at the origin. Also, the root mean squared distance of the image points from the origin is sqrt(2). These steps summarize the process for estimating the camera projection matrix.

  1. Normalize the input image point coordinates with transform T.

  2. Estimate camera projection matrix CN from the normalized input image points.

  3. Compute the denormalized camera projection matrix C as CNT-1.

  4. Compute the reprojected image point coordinates xE as CX.

  5. Compute the reprojection errors as

    reprojectionErrors = |x− xE|.

References

[1] Hartley, Richard, and Andrew Zisserman. Multiple View Geometry in Computer Vision. 2nd ed. Cambridge, UK ; New York: Cambridge University Press, 2003.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2022b

expand all

See Also

Apps

Functions

Topics