View Network Behavior Using tsne

Download Data Set

This example uses the Example Food Images data set, which contains 978 photographs of food in nine classes and is approximately 77 MB in size. Download the data set into your temporary directory by calling the downloadExampleFoodImagesData helper function; the code for this helper function appears at the end of this example.

dataDir = fullfile(tempdir,"ExampleFoodImageDataset");
url = "https://www.mathworks.com/supportfiles/nnet/data/ExampleFoodImageDataset.zip";

if ~exist(dataDir,"dir")
    mkdir(dataDir);
end

downloadExampleFoodImagesData(url,dataDir);

Downloading MathWorks Example Food Image dataset...
This can take several minutes to download...
Download finished...
Unzipping file...
Unzipping finished...
Done.

Train Network to Classify Food Images

Create an imageDatastore containing paths to the image data. Split the datastore into training and validation sets, using 65% of the data for training and the rest for validation. Because the data set is fairly small, overfitting is a significant issue. To minimize overfitting, augment the training set with random flips and scaling.

imds = imageDatastore(dataDir, ...
    IncludeSubfolders=true,LabelSource="foldernames");

aug = imageDataAugmenter(RandXReflection=true, ...
    RandYReflection=true, ...
    RandXScale=[0.8 1.2], ...
    RandYScale=[0.8 1.2]);

trainingFraction = 0.65;
[trainImds,valImds] = splitEachLabel(imds,trainingFraction);

augImdsTrain = augmentedImageDatastore([227 227],trainImds, ...
    DataAugmentation=aug);
augImdsVal = augmentedImageDatastore([227 227],valImds);
classNames = categories(trainImds.Labels);
numClasses = numel(classNames);

Load a pretrained SqueezeNet network and the corresponding class names. This requires the Deep Learning Toolbox™ Model for SqueezeNet Network support package. If this support package is not installed, then the software provides a download link. For a list of all available networks, see Pretrained Deep Neural Networks. To return a neural network ready for retraining for the new data, also specify the number of classes.

net = imagePretrainedNetwork("squeezenet",NumClasses=numClasses);

Create training options.

opts = trainingOptions("adam", ...
    InitialLearnRate=1e-4, ...
    MaxEpochs=50, ...
    ValidationData=augImdsVal, ...
    Verbose=false,...
    Plots="training-progress", ...
    MiniBatchSize=128,...
    Metrics="accuracy");
rng default

Train the neural network using the trainnet function. For classification, use the cross-entropy loss function. By default, the trainnet function uses a GPU if one is available. Training on a GPU requires a Parallel Computing Toolbox™ license and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox). Otherwise, the trainnet function uses the CPU.

net = trainnet(augImdsTrain,net,"crossentropy",opts);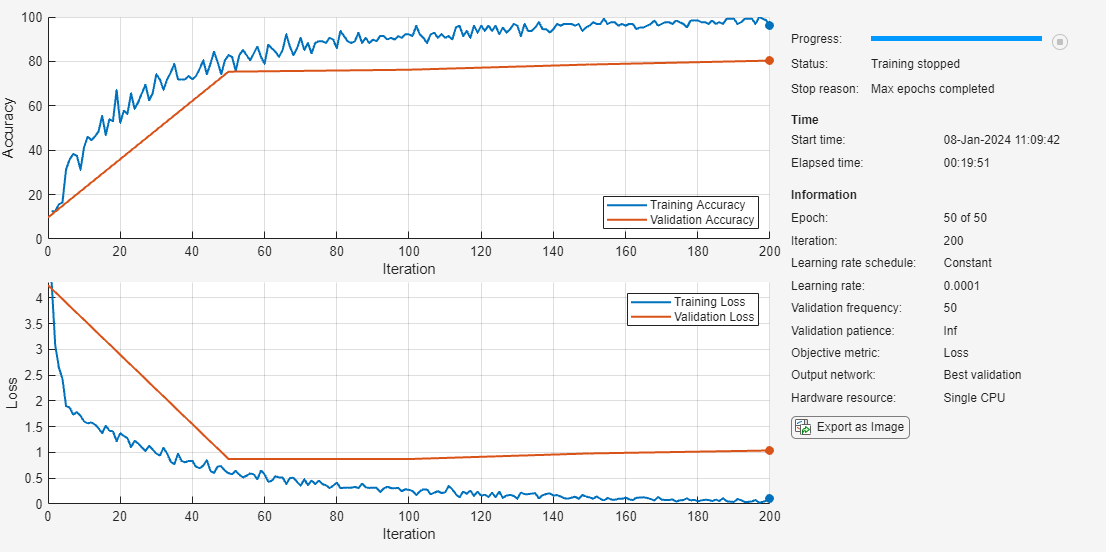

Classify Validation Data

Classify the test images. To make predictions with multiple observations, use the minibatchpredict function. To convert the prediction scores to labels, use the scores2label function. The minibatchpredict function automatically uses a GPU if one is available. Using a GPU requires a Parallel Computing Toolbox™ license and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox). Otherwise, the function uses the CPU.

figure();
scores = minibatchpredict(net,augImdsVal);
YPred = scores2label(scores,classNames);

confusionchart(valImds.Labels,YPred,ColumnSummary="column-normalized")

The network classifies several images well. The network appears to have trouble with sushi images, classifying many as sushi but some as pizza or hamburger. The network does not classify any images into the hot dog class.

Compute Activations for Several Layers

To continue to analyze the network performance, compute activations for every observation in the data set at an early max pooling layer, the final convolutional layer, and the final softmax layer. Output the activations as an NxM matrix, where N is the number of observations and M is the number of dimensions of the activation. M is the product of spatial and channel dimensions. Each row is an observation, and each column is a dimension. At the softmax layer M = 9, because the food data set has nine classes. Each row in the matrix contains nine elements, corresponding to the probabilities that an observation belongs to each of the nine classes of food.

earlyLayerName = "pool1";
finalConvLayerName = "conv10";
softmaxLayerName = "prob_flatten";
pool1Activations = minibatchpredict(net,...
    augImdsVal,Outputs=earlyLayerName);
finalConvActivations = minibatchpredict(net,...
    augImdsVal,Outputs=finalConvLayerName);
softmaxActivations = minibatchpredict(net,...
    augImdsVal,Outputs=softmaxLayerName);

Reshape activation matrices in 2-D. The t-SNE function requires 2-D inputs.

numValObservations = augImdsVal.numobservations;
pool1Activations = reshape(pool1Activations,numValObservations,[]);
finalConvActivations = reshape(finalConvActivations,numValObservations,[]);
softmaxActivations = reshape(softmaxActivations,numValObservations,[]);

Ambiguity of Classifications

You can use the softmax activations to calculate the image classifications that are most likely to be incorrect. Define the ambiguity of a classification as the ratio of the second-largest probability to the largest probability. The ambiguity of a classification is between zero (nearly certain classification) and 1 (nearly as likely to be classified to the most likely class as the second class). An ambiguity of near 1 means the network is unsure of the class in which a particular image belongs. This uncertainty might be caused by two classes whose observations appear so similar to the network that it cannot learn the differences between them. Or, a high ambiguity can occur because a particular observation contains elements of more than one class, so the network cannot decide which classification is correct. Note that low ambiguity does not necessarily imply correct classification; even if the network has a high probability for a class, the classification can still be incorrect.

[R,RI] = maxk(softmaxActivations,2,2);
ambiguity = R(:,2)./R(:,1);

Find the most ambiguous images.

[ambiguity,ambiguityIdx] = sort(ambiguity,"descend");

View the most probable classes of the ambiguous images and the true classes.

classList = unique(valImds.Labels);
top10Idx = ambiguityIdx(1:10);
top10Ambiguity = ambiguity(1:10);
mostLikely = classList(RI(ambiguityIdx,1));
secondLikely = classList(RI(ambiguityIdx,2));
table(top10Idx,top10Ambiguity,mostLikely(1:10),secondLikely(1:10),valImds.Labels(ambiguityIdx(1:10)),...
    VariableNames=["Image #","Ambiguity","Likeliest","Second","True Class"])

ans=10×5 table
    Image #    Ambiguity     Likeliest        Second         True Class 
    _______    _________    ___________    _____________    ____________

      180       0.96684     sashimi        pizza            pizza       
       26       0.95833     sushi          pizza            french_fries
      291       0.92104     sashimi        hamburger        sashimi     
      286       0.91898     pizza          hot_dog          sashimi     
      322       0.88626     hot_dog        sushi            sushi       
       89       0.87801     hamburger      french_fries     hamburger   
      242        0.8727     greek_salad    sushi            pizza       
       84       0.85619     greek_salad    sushi            greek_salad 
      245       0.85266     greek_salad    pizza            pizza       
      145       0.84436     sushi          caprese_salad    hamburger   

The network predicts that image 27 is most likely hamburger or pizza. However, this image is actually French fries. View the image to see why this misclassification might occur.

v = 27;
figure();
imshow(valImds.Files{v});
title(sprintf("Observation: %i\n" + ...
    "Actual: %s. Predicted: %s", v, ...
    string(valImds.Labels(v)),string(YPred(v))), ...
    Interpreter="none");

The image contains several distinct regions, some of which might confuse the network.

Compute 2-D Representations of Data Using t-SNE

Calculate a low-dimensional representation of the network data for an early max pooling layer, the final convolutional layer, and the final softmax layer. Use the tsne function to reduce the dimensionality of the activation data from M to 2. The larger the dimensionality of the activations, the longer the t-SNE computation takes. Therefore, computation for the early max pooling layer, where activations have 200,704 dimensions, takes longer than for the final softmax layer. Set the random seed for reproducibility of the t-SNE result.

rng default
pool1tsne = tsne(pool1Activations);
finalConvtsne = tsne(finalConvActivations);
softmaxtsne = tsne(softmaxActivations);

Compare Network Behavior for Early and Later Layers

The t-SNE technique tries to preserve distances so that points near each other in the high-dimensional representation are also near each other in the low-dimensional representation. As shown in the confusion matrix, the network is effective at classifying into different classes. Therefore, images that are semantically similar (or of the same type), such as caesar salad and caprese salad, are near each other in the softmax activations space. t-SNE captures this proximity in a 2-D representation that is easier to understand and plot than the nine-dimensional softmax scores.

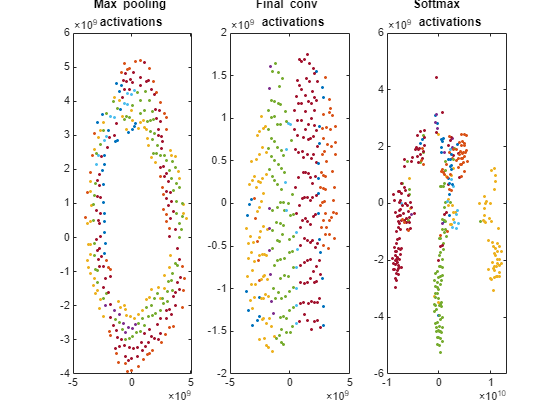
Early layers tend to operate on low-level features such as edges and colors. Deeper layers have learned high-level features with more semantic meaning, such as the difference between a pizza and a hot dog. Therefore, activations from early layers do not show any clustering by class. Two images that are similar pixelwise (for example, they both contain a lot of green pixels) are near each other in the high-dimensional space of the activations, regardless of their semantic contents. Activations from later layers tend to cluster points from the same class together. This behavior is most pronounced at the softmax layer and is preserved in the two-dimensional t-SNE representation.

Plot the t-SNE data for the early max pooling layer, the final convolutional layer, and the final softmax layer using the gscatter function. Observe that the early max pooling activations do not exhibit any clustering between images of the same class. Activations of the final convolutional layer are clustered by class to some extent, but less so than the softmax activations. Different colors correspond to observations of different classes.

doLegend = "off";
markerSize = 7;
figure;

subplot(1,3,1);
gscatter(pool1tsne(:,1),pool1tsne(:,2),valImds.Labels, ...
    [],'.',markerSize,doLegend);
title("Max pooling \newline activations");

subplot(1,3,2);
gscatter(finalConvtsne(:,1),finalConvtsne(:,2),valImds.Labels, ...
    [],'.',markerSize,doLegend);
title("Final conv \newline activations");

subplot(1,3,3);
gscatter(softmaxtsne(:,1),softmaxtsne(:,2),valImds.Labels, ...
    [],'.',markerSize,doLegend);
title("Softmax \newline activations");

Explore Observations in t-SNE Plot

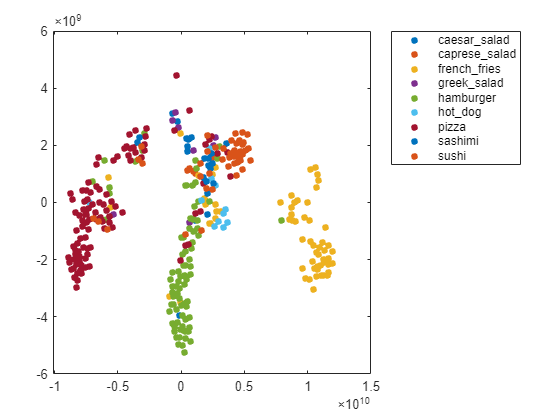
Create a larger plot of the softmax activations, including a legend labeling each class. From the t-SNE plot, you can understand more about the structure of the posterior probability distribution.

For example, the plot shows a distinct, separate cluster of French fries observations, whereas the sashimi and sushi clusters are not resolved very well. Similar to the confusion matrix, the plot suggests that the network is more accurate at predicting into the French fries class.

numClasses = length(classList);
colors = lines(numClasses);
h = figure;
gscatter(softmaxtsne(:,1),softmaxtsne(:,2),valImds.Labels,colors);

l = legend;
l.Interpreter = "none";
l.Location = "bestoutside";

You can also use t-SNE to determine which images are misclassified by the network and why. Incorrect observations are often isolated points of the wrong color for their surrounding cluster. For example, a misclassified image of hamburger is very near the French fries region (the green dot nearest the center of the orange cluster). This dot is observation 99. Circle this observation on the t-SNE plot, and display the image with imshow.

obs = 99;
figure(h)
hold on;
hs = scatter(softmaxtsne(obs, 1), softmaxtsne(obs, 2), ...
    'black',LineWidth=1.5);
l.String{end} = "Hamburger";
hold off;
figure();
imshow(valImds.Files{obs});
title(sprintf("Observation: %i\n" + ...
    "Actual: %s. Predicted: %s",obs, ...
    string(valImds.Labels(obs)),string(YPred(obs))), ...
    Interpreter="none");

If an image contains multiple types of food, the network can get confused. In this case, the network classifies the image as French fries even though the food in the foreground is hamburger. The French fries visible at the edge of the image cause the confusion.

Similarly, the ambiguous image 27 (shown earlier in the example) has multiple regions. Examine the t-SNE plot highlighting the ambiguous aspect of this French fries image.

obs = 27;
figure(h)
hold on;
h = scatter(softmaxtsne(obs, 1), softmaxtsne(obs, 2), ...
    'k','d',LineWidth=1.5);
l.String{end} = "French Fries";
hold off;

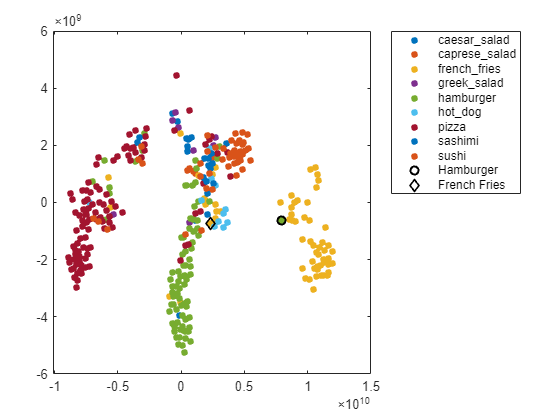
The image is not in a well-defined cluster in the plot, which indicates that the classification is likely incorrect. The image is far from the French fries cluster, and close to the hamburger cluster.

The why of a misclassification must be provided by other information, typically a hypothesis based on the contents of the image. You can then test the hypothesis using other data, or using tools that indicate which spatial regions of an image are important to network classification. For examples, see occlusionSensitivity and Grad-CAM Reveals the Why Behind Deep Learning Decisions.

References

[1] van der Maaten, Laurens, and Geoffrey Hinton. "Visualizing Data using t-SNE." Journal of Machine Learning Research 9, 2008, pp. 2579–2605.

Helper Function

function downloadExampleFoodImagesData(url, dataDir)
% Download the Example Food Image data set, containing 978 images of
% different types of food split into 9 classes.

% Copyright 2019 The MathWorks, Inc.

fileName = "ExampleFoodImageDataset.zip";
fileFullPath = fullfile(dataDir, fileName);

% Download the .zip file into a temporary directory.
if ~exist(fileFullPath, "file")
    fprintf("Downloading MathWorks Example Food Image dataset...\n");
    fprintf("This can take several minutes to download...\n");
    websave(fileFullPath, url);
    fprintf("Download finished...\n");
else
    fprintf("Skipping download, file already exists...\n");
end

% Unzip the file.
%
% Check if the file has already been unzipped by checking for the presence
% of one of the class directories.
exampleFolderFullPath = fullfile(dataDir, "pizza");
if ~exist(exampleFolderFullPath, "dir")
    fprintf("Unzipping file...\n");
    unzip(fileFullPath, dataDir);
    fprintf("Unzipping finished...\n");
else
    fprintf("Skipping unzipping, file already unzipped...\n");
end
fprintf("Done.\n");

end