Main Content

portsim

Monte Carlo simulation of correlated asset returns

collapse all in page

Syntax

RetSeries = portsim(ExpReturn,ExpCovariance,NumObs)
RetSeries = portsim(___,RetIntervals,NumSim,Method)

Description

RetSeries = portsim(ExpReturn,ExpCovariance,NumObs) simulates correlated returns of NASSETS assets over NUMOBS consecutive observation intervals. Asset returns are simulated as the proportional increments of constant drift, constant volatility stochastic processes, thereby approximating continuous-time geometric Brownian motion.

Note

An alternative for portfolio optimization is to use the Portfolio object for mean-variance portfolio optimization. This object supports gross or net portfolio returns as the return proxy, the variance of portfolio returns as the risk proxy, and a portfolio set that is any combination of the specified constraints to form a portfolio set. For information on the workflow when using Portfolio objects, see Portfolio Object Workflow.

example

RetSeries = portsim(___,RetIntervals,NumSim,Method) specifies options using one or more optional arguments in addition to the input arguments in the previous syntax.

example

Examples

collapse all

Open Live Script

This example shows the distinction between the Exact and Expected methods of simulation.

Consider a portfolio of five assets with the following expected returns, standard deviations, and correlation matrix based on daily asset returns (where ExpReturn and Sigmas are divided by 100 to convert percentages to returns). 

ExpReturn     = [0.0246  0.0189  0.0273  0.0141  0.0311]/100;
Sigmas        = [0.9509  1.4259  1.5227  1.1062  1.0877]/100;
Correlations  = [1.0000  0.4403  0.4735  0.4334  0.6855
                 0.4403  1.0000  0.7597  0.7809  0.4343
                 0.4735  0.7597  1.0000  0.6978  0.4926
                 0.4334  0.7809  0.6978  1.0000  0.4289
                 0.6855  0.4343  0.4926  0.4289  1.0000];

Convert the correlations and standard deviations to a covariance matrix. 

ExpCovariance = corr2cov(Sigmas, Correlations)
ExpCovariance = 5×5
10-3 ×

    0.0904    0.0597    0.0686    0.0456    0.0709
    0.0597    0.2033    0.1649    0.1232    0.0674
    0.0686    0.1649    0.2319    0.1175    0.0816
    0.0456    0.1232    0.1175    0.1224    0.0516
    0.0709    0.0674    0.0816    0.0516    0.1183

Assume that there are 252 trading days in a calendar year, and simulate two sample paths (realizations) of daily returns over a two-year period. Since ExpReturn and ExpCovariance are expressed daily, set RetIntervals = 1. 

StartPrice    = 100;
NumObs        = 504;  % two calendar years of daily returns
NumSim        = 2;
RetIntervals  = 1;    % one trading day
NumAssets     = 5;

To illustrate the distinction between methods, simulate two paths by each method, starting with the same random number state. 

rng('default'); 
RetExact = portsim(ExpReturn, ExpCovariance, NumObs, ... 
RetIntervals, NumSim, 'Exact');
rng(0); 
RetExpected = portsim(ExpReturn, ExpCovariance, NumObs, ... 
RetIntervals, NumSim, 'Expected');

Compare the mean and covariance of RetExact with the inputs (ExpReturn and ExpCovariance), you will observe that they are almost identical.

At this point, RetExact and RetExpected are both 504-by-5-by-2 arrays. Now assume an equally weighted portfolio formed from the five assets and create arrays of portfolio returns in which each column represents the portfolio return of the corresponding sample path of the simulated returns of the five assets. The portfolio arrays PortRetExact and PortRetExpected are 504-by-2 matrices. 

Weights         = ones(NumAssets, 1)/NumAssets;
PortRetExact    = zeros(NumObs, NumSim);
PortRetExpected = zeros(NumObs, NumSim);

for i = 1:NumSim
    PortRetExact(:,i)    = RetExact(:,:,i) * Weights;
    PortRetExpected(:,i) = RetExpected(:,:,i) * Weights; 
end

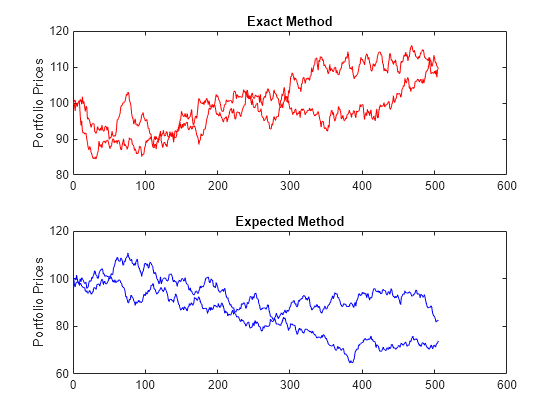
Finally, convert the simulated portfolio returns to prices and plot the data. In particular, note that since the Exact method matches expected return and covariance, the terminal portfolio prices are virtually identical for each sample path. This is not true for the Expected simulation method. Although this example examines portfolios, the same methods apply to individual assets as well. Thus, Exact simulation is most appropriate when unique paths are required to reach the same terminal prices. 

PortExact   = ret2tick(PortRetExact, ... 
repmat(StartPrice,1,NumSim)); 
PortExpected = ret2tick(PortRetExpected, ... 
repmat(StartPrice,1,NumSim)); 
subplot(2,1,1), plot(PortExact, '-r')
ylabel('Portfolio Prices')
title('Exact Method')
subplot(2,1,2), plot(PortExpected, '-b')
ylabel('Portfolio Prices')
title('Expected Method')

Figure contains 2 axes objects. Axes object 1 with title Exact Method, ylabel Portfolio Prices contains 2 objects of type line. Axes object 2 with title Expected Method, ylabel Portfolio Prices contains 2 objects of type line.

This example shows the interplay among ExpReturn, ExpCovariance, and RetIntervals. Recall that portsim simulates correlated asset returns over an interval of length dt, given by the equation

dSS=μdt+σdz=μdt+σεdt,

where S is the asset price, μ is the expected rate of return, σ is the volatility of the asset price, and ε represents a random drawing from a standardized normal distribution.

The time increment dt is determined by the optional input RetIntervals, either as an explicit input argument or as a unit time increment by default. Regardless, the periodicity of ExpReturn, ExpCovariance, and RetIntervals must be consistent. For example, if ExpReturn and ExpCovariance are annualized, then RetIntervals must be in years. This point is often misunderstood.

To illustrate the interplay among ExpReturn, ExpCovariance, and RetIntervals, consider a portfolio of five assets with the following expected returns, standard deviations, and correlation matrix based on daily asset returns.

ExpReturn     = [0.0246  0.0189  0.0273  0.0141  0.0311]/100;

Sigmas        = [0.9509  1.4259  1.5227  1.1062  1.0877]/100;

Correlations  = [1.0000  0.4403  0.4735  0.4334  0.6855
                 0.4403  1.0000  0.7597  0.7809  0.4343
                 0.4735  0.7597  1.0000  0.6978  0.4926
                 0.4334  0.7809  0.6978  1.0000  0.4289
                 0.6855  0.4343  0.4926  0.4289  1.0000];

Convert the correlations and standard deviations to a covariance matrix of daily returns.

 ExpCovariance = corr2cov(Sigmas, Correlations);

Assume 252 trading days per calendar year, and simulate a single sample path of daily returns over a four-year period. Since the ExpReturn and ExpCovariance inputs are expressed daily, set RetIntervals = 1.

StartPrice    = 100;
NumObs        = 1008;   % four calendar years of daily returns
RetIntervals  = 1;      % one trading day
NumAssets     = length(ExpReturn);
randn('state',0);
RetSeries1 = portsim(ExpReturn, ExpCovariance, NumObs, ... 
RetIntervals, 1, 'Expected');

Now annualize the daily data, thereby changing the periodicity of the data, by multiplying ExpReturn and ExpCovariance by 252 and dividing RetIntervals by 252 (RetIntervals = 1/252 of a year). Resetting the random number generator to its initial state, you can reproduce the results.

rng('default'); 
RetSeries2 = portsim(ExpReturn*252, ExpCovariance*252, ... 
NumObs, RetIntervals/252, 1, 'Expected');

Assume an equally weighted portfolio and compute portfolio returns associated with each simulated return series.

Weights  = ones(NumAssets, 1)/NumAssets;

PortRet1 = RetSeries2 * Weights;
PortRet2 = RetSeries2 * Weights;

Comparison of the data reveals that PortRet1 and PortRet2 are identical.

This example shows how to simulate a univariate geometric Brownian motion process. It is based on an example found in Hull, Options, Futures, and Other Derivatives, 5th Edition (see example 12.2 on page 236). In addition to verifying Hull's example, it also graphically illustrates the lognormal property of terminal stock prices by a rather large Monte Carlo simulation.

Assume that you own a stock with an initial price of $20, an annualized expected return of 20% and volatility of 40%. Simulate the daily price process for this stock over the course of one full calendar year (252 trading days).

StartPrice    = 20;
ExpReturn     = 0.2; 
ExpCovariance = 0.4^2;
NumObs        = 252;
NumSim        = 10000;
RetIntervals  = 1/252;

RetIntervals is expressed in years, consistent with the fact that ExpReturn and ExpCovariance are annualized. Also, ExpCovariance is entered as a variance rather than the more familiar standard deviation (volatility).

Set the random number generator state, and simulate 10,000 trials (realizations) of stock returns over a full calendar year of 252 trading days. 

rng('default');
RetSeries = squeeze(portsim(ExpReturn, ExpCovariance, NumObs, ... 
RetIntervals, NumSim, 'Expected'));

The squeeze function reformats the output array of simulated returns from a 252-by-1-by-10000 array to more convenient 252-by-10000 array. (Recall that portsim is fundamentally a multivariate simulation engine).

In accordance with Hull's equations 12.4 and 12.5 on page 236

E(ST)=S0eμTvar(ST)=S02e2μT(eσ2T−1)

convert the simulated return series to a price series and compute the sample mean and the variance of the terminal stock prices. 

StockPrices = ret2tick(RetSeries, repmat(StartPrice, 1, NumSim));

SampMean = mean(StockPrices(end,:))
SampVar = var(StockPrices(end,:))
SampMean =

   24.4489


SampVar =

  101.4243

Compare these values with the values you obtain by using Hull's equations.

ExpValue = StartPrice*exp(ExpReturn)
ExpVar = ... 
StartPrice*StartPrice*exp(2*ExpReturn)*(exp((ExpCovariance)) - 1)
ExpValue =

   24.4281


ExpVar =

  103.5391

These results are very close to the results shown in Hull's example 12.2.

Display the sample density function of the terminal stock price after one calendar year. From the sample density function, the lognormal distribution of terminal stock prices is apparent.

[count, BinCenter] = hist(StockPrices(end,:), 30);
figure
bar(BinCenter, count/sum(count), 1, 'r')
xlabel('Terminal Stock Price')
ylabel('Probability')
title('Lognormal Terminal Stock Prices')

Input Arguments

collapse all

Expected (mean) return of each asset, specified as a 1-by-NASSETS vector.

Data Types: double

Asset return covariances, specified as an NASSETS-by-NASSETS matrix. ExpCovariance must be symmetric and positive semidefinite (no negative eigenvalues). The standard deviations of the returns are ExpSigma = sqrt(diag(ExpCovariance)). If ExpCovariance is not a symmetric positive semidefinite matrix, use nearcorr to create a positive semidefinite matrix for a correlation matrix.

Data Types: double

number of consecutive observations in the return time series, specified as a positive scalar integer. If NumObs is entered as the empty matrix [], the length of RetIntervals is used.

Data Types: double

(Optional) Interval times between observations, specified as a positive scalar or a number of observations NUMOBS-by-1 vector. If RetIntervals is not specified, all intervals are assumed to have length 1.

Data Types: double

(Optional) Number of simulated sample paths (realizations) of NUMOBS observations, specified as a positive scalar integer. The default value for NumSim is 1 (single realization of NUMOBS correlated asset returns).

Data Types: double

(Optional) Type of Monte Carlo simulation, specified as a character vector with one of the following values:

  • 'Exact' (default) generates correlated asset returns in which the sample mean and covariance match the input mean (ExpReturn) and covariance (ExpCovariance) specifications.

  • 'Expected' generates correlated asset returns in which the sample mean and covariance are statistically equal to the input mean and covariance specifications. (The expected values of the sample mean and covariance are equal to the input mean (ExpReturn) and covariance (ExpCovariance) specifications.)

For either Method, the sample mean and covariance returned are appropriately scaled by RetIntervals.

Data Types: char

Output Arguments

collapse all

Three-dimensional array of correlated, normally distributed, proportional asset returns, returned as a NUMOBS-by-NASSETS-by-NUMSIM three-dimensional array.

Asset returns over an interval of length dt are given by

dSS=μdt+σdz=μdt+σεdt,

where S is the asset price, μ is the expected rate of return, σ is the volatility of the asset price, and ε represents a random drawing from a standardized normal distribution.

Notes

  • When Method is 'Exact', the sample mean and covariance of all realizations (scaled by RetIntervals) match the input mean and covariance. When the returns are then converted to asset prices, all terminal prices for a given asset are in close agreement. Although all realizations are drawn independently, they produce similar terminal asset prices. Set Method to 'Expected' to avoid this behavior.

  • The returns from the portfolios in PortWts are given by PortReturn = PortWts * RetSeries(:,:,1)', where PortWts is a matrix in which each row contains the asset allocations of a portfolio. Each row of PortReturn corresponds to one of the portfolios identified in PortWts, and each column corresponds to one of the observations taken from the first realization (the first plane) in RetSeries. See portopt and portstats for portfolio specification and optimization.

References

[1] Hull, J. C. Options, Futures, and Other Derivatives. Prentice-Hall, 2003.

Version History

Introduced before R2006a

See Also

| | | | | |

Topics