b0 = 0.05634;
b1 = [1  1];
b2 = [1 -1.0166 1];
a1 = [1 -0.683];
a2 = [1 -1.4461 0.7957];

b = b0*conv(b1,b2);
a = conv(a1,a2);

[h,w] = freqz(b,a,'whole',2001);

绘制以分贝表示的幅值响应。

plot(w/pi,20*log10(abs(h)))
ax = gca;
ax.YLim = [-100 20];
ax.XTick = 0:.5:2;
xlabel('Normalized Frequency (\times\pi rad/sample)')
ylabel('Magnitude (dB)')

Figure contains an axes object. The axes object with xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Magnitude (dB) contains an object of type line.

级联传递函数的频率响应

自 R2024b 起

打开实时脚本

设计一个 40 阶低通切比雪夫 II 型数字滤波器，阻带边缘频率为 0.4，阻带衰减为 50 dB。使用 CTF 格式的滤波器的系数绘制滤波器的频率响应。

[B,A] = cheby2(40,50,0.4,"ctf");

freqz(B,A,"ctf")

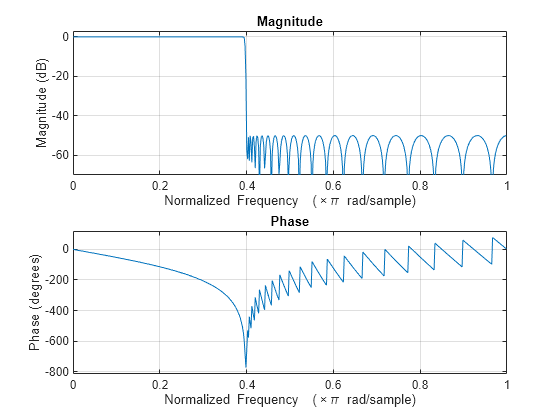
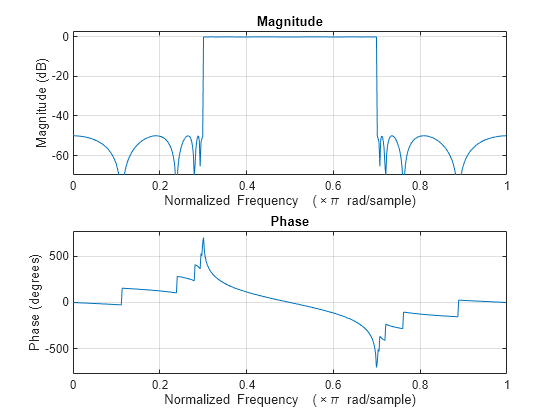
$Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.$

设计一个 30 阶带通椭圆数字滤波器，通带边缘频率为 0.3 和 0.7，通带波纹为 0.1 dB，阻带衰减为 50 dB。使用 CTF 格式的滤波器的系数和增益，绘制滤波器的频率响应。

[B,A,g] = ellip(30,0.1,50,[0.3 0.7],"ctf");
freqz({B,A,g},"ctf")

FIR 滤波器的频率响应

打开实时脚本

使用 $β = 8$ 的凯塞窗设计 80 阶 FIR 低通滤波器。指定归一化截止频率为 $0.5 π$ 弧度/采样点。显示滤波器的幅值和相位响应。

b = fir1(80,0.5,kaiser(81,8));
freqz(b,1)

使用 designfilt 设计相同的滤波器。显示其幅值和相位响应。

d = designfilt("lowpassfir",FilterOrder=80, ...
    CutoffFrequency=0.5,Window={"kaiser",8});
freqz(d)

FIR 带通滤波器的频率响应

打开实时脚本

设计一个 FIR 带通滤波器，通带在 $0.35 π$ 和 $0.8 π$ 弧度/采样点之间，波纹为 3 dB。第一个阻带是从 $0$ 到 $0.1 π$ 弧度/采样点，衰减为 40 dB。第二个阻带是从 $0.9 π$ 弧度/采样点到奈奎斯特频率，衰减为 30 dB。计算频率响应。同时以线性单位和分贝绘制其幅值。突出显示通带。

sf1 = 0.1;
pf1 = 0.35;
pf2 = 0.8;
sf2 = 0.9;
pb = linspace(pf1,pf2,1e3)*pi;

bp = designfilt("bandpassfir", ...
    StopbandAttenuation1=40,StopbandFrequency1=sf1, ...
    PassbandFrequency1=pf1,PassbandRipple=3, ...
    PassbandFrequency2=pf2,StopbandFrequency2=sf2, ...
    StopbandAttenuation2=30);

[h,w] = freqz(bp,1024);
hpb = freqz(bp,pb);

subplot(2,1,1)
plot(w/pi,abs(h),pb/pi,abs(hpb),'.-')
axis([0 1 -1 2])
legend("Response","Passband",Location="south")
ylabel("Magnitude")

subplot(2,1,2)
plot(w/pi,db(h),pb/pi,db(hpb),".-")
axis([0 1 -60 10])
xlabel("Normalized Frequency (\times\pi rad/sample)")
ylabel("Magnitude (dB)")

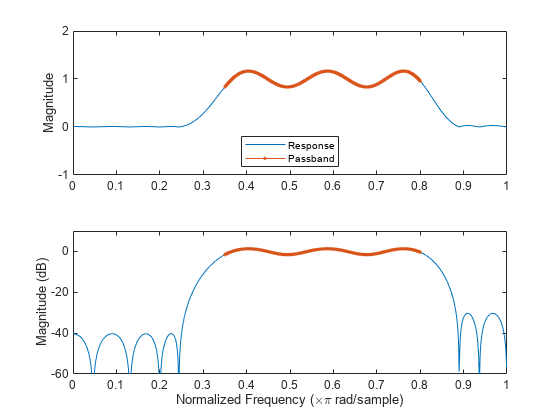
$Figure contains 2 axes objects. Axes object 1 with ylabel Magnitude contains 2 objects of type line. These objects represent Response, Passband. Axes object 2 with xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains 2 objects of type line.$

二阶节的频率响应

打开实时脚本

计算并显示由以下传递函数描述的三阶 IIR 低通滤波器的幅值响应：

$H (z) = \frac{0.05634 (1 + z^{- 1}) (1 - 1.0166 z^{- 1} + z^{- 2})}{(1 - 0.683 z^{- 1}) (1 - 1.4461 z^{- 1} + 0.7957 z^{- 2})} .$

用二阶节表示传递函数。求分布在整个单位圆上的 2001 个点上的频率响应。

b0 = 0.05634;
b1 = [1  1];
b2 = [1 -1.0166 1];
a1 = [1 -0.683];
a2 = [1 -1.4461 0.7957];

sos1 = [b0*[b1 0] [a1 0]];
sos2 = [b2 a2];

[h,w] = freqz([sos1;sos2],'whole',2001);

绘制以分贝表示的幅值响应。

plot(w/pi,20*log10(abs(h)))
ax = gca;
ax.YLim = [-100 20];
ax.XTick = 0:.5:2;
xlabel('Normalized Frequency (\times\pi rad/sample)')
ylabel('Magnitude (dB)')

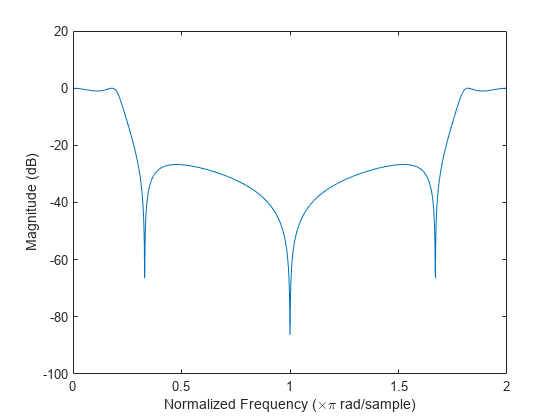
Figure contains an axes object. The axes object with xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Magnitude (dB) contains an object of type line.

输入参数

全部折叠

`b`, `a` — 传递函数系数
向量

传递函数系数，指定为向量。用 b 和 a 将传递函数表示为

$H (z) = \frac{B (z)}{A (z)} = \frac{b_{1} + b_{2} z^{- 1} \dots + b_{n} z^{- (n - 1)} + b_{n + 1} z^{- n}}{a_{1} + a_{2} z^{- 1} \dots + a_{m} z^{- (m - 1)} + a_{m + 1} z^{- m}}$

示例: b = [1 3 3 1]/6 和 a = [3 0 1 0]/3 用于指定归一化 3 dB 频率为 0.5π 弧度/采样点的三阶巴特沃斯滤波器。

数据类型: double | single
复数支持: 是

`n` — 要在其上计算响应的频率点的数量
512 (默认) | 正整数标量

要在其上计算响应的频率点的数量，指定为不小于 2 的正整数标量。当 n 不存在时，它默认为 512。为了获得最佳效果，请将 n 设置为大于滤波器阶数的值。

`B,A` — 级联传递函数 (CTF) 系数
标量 | 向量 | 矩阵

自 R2024b 起

级联传递函数 (CTF) 系数，指定为标量、向量或矩阵。B 和 A 分别列出级联传递函数的分子系数和分母系数。

B 的大小必须为 L×(m + 1)，A 的大小必须为 L×(n + 1)，其中：

L 表示滤波器节的数量。
m 表示滤波器分子的阶。
n 表示滤波器分母的阶。

有关级联传递函数格式和系数矩阵的详细信息，请参阅以 CTF 格式指定数字滤波器。

注意

如果 A(:,1) 的任一元素不等于 1，则 freqz 按 A(:,1) 对滤波器系数进行归一化。在这种情况下，A(:,1) 必须为非零。

数据类型: double | single
复数支持: 是

`g` — 尺度值
标量 | 向量

自 R2024b 起

尺度值，指定为具有 L + 1 个元素的实数值标量或实数值向量，其中 L 是 CTF 节的数量。尺度值表示滤波器增益在级联滤波器表示的各节之间的分布。

freqz 函数使用 scaleFilterSections 函数将增益应用于滤波器节，具体取决于您如何指定 g：

标量 - 函数将增益均匀分布在所有滤波器节上。
向量 - 函数将前 L 个增益值应用于对应的滤波器节，并将最后一个增益值均匀分布在所有滤波器节上。

数据类型: double | single

`d` — 数字滤波器
`digitalFilter` 对象

数字滤波器，指定为 digitalFilter 对象。使用 designfilt 根据频率响应设定生成数字滤波器。

示例: d = designfilt('lowpassiir','FilterOrder',3,'HalfPowerFrequency',0.5) 用于指定归一化 3 dB 频率为 0.5π 弧度/采样点的三阶巴特沃斯滤波器。

`sos` — 二阶节系数
矩阵

二阶节系数，指定为矩阵。sos 是 K×6 矩阵，其中节数 K 必须大于或等于 2。如果节数小于 2，该函数将输入视为分子向量。sos 的每行对应于二阶 (biquad) 滤波器的系数。sos 的第 i 行对应于 [bi(1) bi(2) bi(3) ai(1) ai(2) ai(3)]。

示例: s = [2 4 2 6 0 2;3 3 0 6 0 0] 用于指定归一化 3 dB 频率为 0.5π 弧度/采样点的三阶巴特沃斯滤波器。

数据类型: double | single
复数支持: 是

`fs` — 采样率
正标量

采样率，指定为正标量。当时间单位为秒时，fs 以赫兹表示。

数据类型: double

`w` — 角频率
向量

角频率，指定为向量并以弧度/采样点表示。w 必须至少包含两个元素，否则该函数会将其解释为 n。w = π 对应于奈奎斯特频率。

`f` — 频率
向量

频率，指定为向量。f 必须至少包含两个元素，否则该函数会将其解释为 n。当时间单位为秒时，f 以赫兹表示。

数据类型: double

输出参量

全部折叠

`h` — 频率响应
向量

频率响应，以向量形式返回。如果指定 n，则 h 的长度为 n。如果未指定 n，或指定 n 为空向量，则 h 的长度为 512。

如果 freqz 的输入是单精度值，则该函数使用单精度算术运算计算频率响应。输出 h 是单精度值。

`w` — 角频率
向量

角频率，以向量形式返回。w 值的范围是从 0 到 π。如果在输入中指定 'whole'，则 w 中的值的范围是从 0 到 2π。如果指定 n，则 w 的长度为 n。如果未指定 n，或指定 n 为空向量，则 w 的长度为 512。

`f` — 频率
向量

频率，以单位为赫兹的向量形式返回。f 的值的范围是从 0 到 fs/2 Hz。如果在输入中指定 'whole'，则 f 中的值的范围是从 0 到 fs Hz。如果指定 n，则 f 的长度为 n。如果未指定 n，或指定 n 为空向量，则 f 的长度为 512。

详细信息

全部折叠

级联传递函数

将 IIR 数字滤波器划分为级联节可提高其数值稳定性，并降低其对系数量化误差的易感性。以 L 传递函数 H₁(z)、H₂(z)、…、H_L(z) 表示的传递函数 H(z) 的级联形式为

$H (z) = \prod_{l = 1}^{L} H_{l} (z) = H_{1} (z) \times H_{2} (z) \times \dots \times H_{L} (z) .$

以 CTF 格式指定数字滤波器

您可以以 CTF 格式指定数字滤波器，用于分析、可视化和信号滤波。通过列出其系数 B 和 A 来指定滤波器。您还可以通过指定标量或向量 g 来包括各节的滤波器缩放增益。

滤波器系数

如果您将系数指定为 L 行矩阵

$B = [\begin{matrix} b_{11} & b_{12} & \dots & b_{1, m + 1} \\ b_{21} & b_{22} & \dots & b_{2, m + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ b_{L 1} & b_{L 2} & \dots & b_{L, m + 1} \end{matrix}], A = [\begin{matrix} a_{11} & a_{12} & \dots & a_{1, n + 1} \\ a_{21} & a_{22} & \dots & a_{2, n + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{L 1} & a_{L 2} & \dots & a_{L, n + 1} \end{matrix}],$

则假设您已将滤波器指定为一系列 L 级联传递函数，使得滤波器的完整传递函数为

$H (z) = \frac{b_{11} + b_{12} z^{- 1} + \dots + b_{1, m + 1} z^{- m}}{a_{11} + a_{12} z^{- 1} + \dots + a_{1, n + 1} z^{- n}} \times \frac{b_{21} + b_{22} z^{- 1} + \dots + b_{2, m + 1} z^{- m}}{a_{21} + a_{22} z^{- 1} + \dots + a_{2, n + 1} z^{- n}} \times \dots \times \frac{b_{L 1} + b_{L 2} z^{- 1} + \dots + b_{L, m + 1} z^{- m}}{a_{L 1} + a_{L 2} z^{- 1} + \dots + a_{L, n + 1} z^{- n}},$

其中 m ≥ 0 是滤波器的分子阶数，n ≥ 0 是分母阶数。

如果将 B 和 A 都指定为向量，则假设底层系统是一个单节 IIR 滤波器 (L = 1)，其中 B 表示传递函数的分子，A 表示其分母。
如果 B 是标量，则假设滤波器是所有极点 IIR 滤波器的级联，每个节的整体系统增益等于 B。
如果 A 是标量，则假设滤波器是 FIR 滤波器的级联，每个节的整体系统增益等于 1/A。

注意

要将二阶节矩阵转换为级联传递函数，请使用 sos2ctf 函数。
要将零极点增益滤波器表示转换为级联传递函数，请使用 zp2ctf 函数。

系数和增益

如果您有整体缩放增益或从系数值中析出的多个缩放增益，则可以将系数和增益指定为 {B,A,g} 形式的元胞数组。当您使用定点算术来确保每个滤波器节的输出具有相似的振幅水平时，定标滤波器节尤其重要，这有助于避免由于数值精度有限而导致滤波器响应不准确。

增益可以是标量整体增益或节增益向量。

如果增益是标量，则该值均匀地应用于所有级联滤波器节。
如果增益是向量，则它必须比级联中的滤波器节数 L 多一个元素。前 L 个尺度值中的每个值都应用于对应的滤波器节，最后一个值均匀地应用于所有级联滤波器节。

如果将系数矩阵和增益向量指定为

，则假设滤波器系统的传递函数为

$H (z) = g_{S} (g_{1} \frac{b_{11} + b_{12} z^{- 1} + \dots + b_{1, m + 1} z^{- m}}{a_{11} + a_{12} z^{- 1} + \dots + a_{1, n + 1} z^{- n}} \times g_{2} \frac{b_{21} + b_{22} z^{- 1} + \dots + b_{2, m + 1} z^{- m}}{a_{21} + a_{22} z^{- 1} + \dots + a_{2, n + 1} z^{- n}} \times \dots \times g_{L} \frac{b_{L 1} + b_{L 2} z^{- 1} + \dots + b_{L, m + 1} z^{- m}}{a_{L 1} + a_{L 2} z^{- 1} + \dots + a_{L, n + 1} z^{- n}}) .$

提示

您可以获得 CTF 格式的滤波器，包括缩放增益。使用数字 IIR 滤波器设计函数的输出，例如 butter、cheby1、cheby2 和 ellip。在这些函数中指定 "ctf" 滤波器类型参量，并指定返回 B、A 和 g 以获取尺度值。 (自 R2024b 起)
如果您有不可约多速率滤波器，请使用 freqzmr (DSP System Toolbox) 函数在频域中分析该滤波器。有关不可约多速率滤波器的详细信息，请参阅Overview of Multirate Filters (DSP System Toolbox)。 (自 R2024a 起)
freqzmr (DSP System Toolbox) 函数需要 DSP System Toolbox™。 (自 R2024a 起)

算法

数字滤波器的频率响应可以解释为在 z = e^jω [1] 处对传递函数进行求值。

freqz 根据您指定的（实数或复数）分子和分母多项式确定传递函数，并返回数字滤波器的复频率响应 H(e^jω)。频率响应在您使用的语法所确定的采样点处计算。

freqz 通常使用 FFT 算法来计算频率响应，但前提是您不提供频率向量作为输入参量。它将频率响应计算为变换后的分子和分母系数之比，并用零填充至所需长度。

当您提供频率向量作为输入时，freqz 在每个频率点处计算多项式，并将分子响应除以分母响应。为了计算多项式，该函数使用霍纳方法。

参考

[1] Oppenheim, Alan V., and Ronald W. Schafer, with John R. Buck. Discrete-Time Signal Processing. 2nd Ed. Upper Saddle River, NJ: Prentice Hall, 1999.

[2] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

在向 freqz 函数输入 CTF 系数时，您必须在 freqz 语法中包含 "ctf" 输入参量以生成代码。
如果 freqz 的第一个输入在编译时是可变大小矩阵，则它在运行时不能变为向量或空数组。
如果输入 n 在编译时大小可变，则它在运行时不能变为标量或空数组。

版本历史记录

在 R2006a 之前推出

全部展开

R2025a: 使用“创建绘图”实时编辑器任务可视化级联传递函数

您可以在创建绘图实时编辑器任务中使用级联传递函数 (CTF) 以交互方式可视化 freqz 的输出。

R2024b: 使用级联传递函数分析滤波器

freqz 函数支持级联传递函数 (CTF) 格式的输入。

R2023a: 使用创建绘图实时编辑器任务可视化函数输出

您可以使用创建绘图实时编辑器任务以交互方式可视化 freqz 的输出。您可以选择不同图类型并设置可选参数。该任务还会自动生成代码，这些代码成为您的实时脚本的一部分。

另请参阅

App

滤波器分析器 | 滤波器设计工具

函数

abs | angle | ctffilt | designfilt | digitalFilter | fft | filter | freqs | impz | invfreqs | logspace | freqzmr (DSP System Toolbox)

freqz

语法

说明

示例

传递函数的频率响应

级联传递函数的频率响应

FIR 滤波器的频率响应

FIR 带通滤波器的频率响应

二阶节的频率响应

输入参数

b, a — 传递函数系数 向量

n — 要在其上计算响应的频率点的数量 512 (默认) | 正整数标量

B,A — 级联传递函数 (CTF) 系数 标量 | 向量 | 矩阵

g — 尺度值 标量 | 向量

d — 数字滤波器 digitalFilter 对象

sos — 二阶节系数 矩阵

fs — 采样率 正标量

w — 角频率 向量

f — 频率 向量

输出参量

h — 频率响应 向量

w — 角频率 向量

f — 频率 向量

详细信息

级联传递函数

以 CTF 格式指定数字滤波器

提示

算法

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

版本历史记录

R2025a: 使用“创建绘图”实时编辑器任务可视化级联传递函数

R2024b: 使用级联传递函数分析滤波器

R2023a: 使用创建绘图实时编辑器任务可视化函数输出

另请参阅

App

函数

`b`, `a` — 传递函数系数
向量

`n` — 要在其上计算响应的频率点的数量
512 (默认) | 正整数标量

`B,A` — 级联传递函数 (CTF) 系数
标量 | 向量 | 矩阵

`g` — 尺度值
标量 | 向量

`d` — 数字滤波器
`digitalFilter` 对象

`sos` — 二阶节系数
矩阵

`fs` — 采样率
正标量

`w` — 角频率
向量

`f` — 频率
向量

`h` — 频率响应
向量

`w` — 角频率
向量

`f` — 频率
向量

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。