fitlm

mdl = fitlm(tbl) 返回基于表或数据集数组 tbl 中变量拟合的线性回归模型。默认情况下，fitlm 将最后一个变量作为响应变量。

mdl = fitlm(X,y) 返回基于数据矩阵 X 拟合的响应 y 的线性回归模型。

mdl = fitlm(___,modelspec) 使用上述语法中的任何输入参数组合来定义模型设定。

mdl = fitlm(___,Name,Value) 使用一个或多个名称-值对组参数指定附加选项。例如，您可以指定哪些变量是分类变量、执行稳健回归或使用观测值权重。

示例

用矩阵数据拟合线性回归

使用矩阵输入数据集拟合线性回归模型。

加载 carsmall 数据集，它是一个矩阵输入数据集。

load carsmall
X = [Weight,Horsepower,Acceleration];

使用 fitlm 拟合线性回归模型。

mdl = fitlm(X,MPG)

mdl = 
Linear regression model:
    y ~ 1 + x1 + x2 + x3

Estimated Coefficients:
                    Estimate        SE          tStat        pValue  
                   __________    _________    _________    __________

    (Intercept)        47.977       3.8785        12.37    4.8957e-21
    x1             -0.0065416    0.0011274      -5.8023    9.8742e-08
    x2              -0.042943     0.024313      -1.7663       0.08078
    x3              -0.011583      0.19333    -0.059913       0.95236


Number of observations: 93, Error degrees of freedom: 89
Root Mean Squared Error: 4.09
R-squared: 0.752,  Adjusted R-Squared: 0.744
F-statistic vs. constant model: 90, p-value = 7.38e-27

模型显示包括模型公式、估计的系数和模型汇总统计量。

显示信息的模型公式 y ~ 1 + x1 + x2 + x3 对应于 $y = β_{0} + β_{1} X_{1} + β_{2} X_{2} + β_{3} X_{3} + ϵ$ 。

模型显示还显示估计的系数信息，该信息存储在 Coefficients 属性中。显示 Coefficients 属性。

mdl.Coefficients

ans=4×4 table
                    Estimate        SE          tStat        pValue  
                   __________    _________    _________    __________

    (Intercept)        47.977       3.8785        12.37    4.8957e-21
    x1             -0.0065416    0.0011274      -5.8023    9.8742e-08
    x2              -0.042943     0.024313      -1.7663       0.08078
    x3              -0.011583      0.19333    -0.059913       0.95236

Coefficient 属性包括以下几列：

Estimate - 模型中每个对应项的系数估计值。例如，常数项 (intercept) 的估计值为 47.977。
SE - 系数的标准误差。
tStat - 每个系数的 t 统计量，用于基于对应系数不为零的备择假设来检验对应系数为零的原假设（给出了模型中的其他预测变量）。请注意，tStat = Estimate/SE。例如，截距的 t 统计量为 47.977/3.8785 = 12.37。
pValue - 双侧假设检验的 t 统计量的 p 值。例如，x2 的 t 统计量的 p 值大于 0.05，因此在给定模型中其他项的情况下，该项在 5% 显著性水平上不显著。

模型的汇总统计量如下：

Number of observations - 没有任何 NaN 值的行数。例如，Number of observations 为 93，因为 X 和 MPG 中的行数为 100，但 MPG 数据向量有六个 NaN 值，且 Horsepower 数据向量中有另一不同观测值（即不同的行）也为 NaN 值。
Error degrees of freedom - n - p，其中 n 是观测值数目，p 是模型中系数的数目，包括截距。例如，该模型有四个预测变量，因此 Error degrees of freedom 为 93–4 = 89。
Root mean squared error - 均方误差的平方根，用于估计误差分布的标准差。
R-squared 和 Adjusted R-squared - 分别为决定系数和调整决定系数。例如，R-squared 值表明，该模型解释了响应变量 MPG 中大约 75% 的变异。
F-statistic vs. constant model - 对回归模型进行 F 检验的检验统计量，用于检验该模型的拟合是否显著优于仅包含常数项的退化模型。
p-value - 对模型的 F 检验的 p 值。例如，p 值为 7.3816e-27，说明模型是显著的。

您可以使用 anova 函数在模型属性（NumObservations、DFE、RMSE 和 Rsquared）中找到这些统计量。

anova(mdl,'summary')

ans=3×5 table
                SumSq     DF    MeanSq      F         pValue  
                ______    __    ______    ______    __________

    Total       6004.8    92    65.269                        
    Model         4516     3    1505.3    89.987    7.3816e-27
    Residual    1488.8    89    16.728

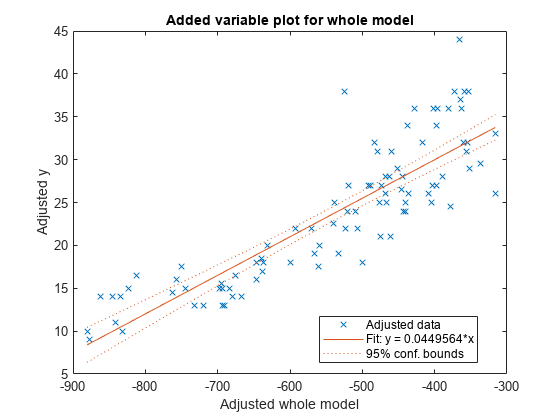
使用 plot 为除常量（截距）项之外的整个模型创建一个变量添加图（偏回归杠杆图）。

plot(mdl)

Figure contains an axes object. The axes object with title Added variable plot for whole model contains 3 objects of type line. These objects represent Adjusted data, Fit: y=0.0449564*x, 95% conf. bounds.

使用表中的数据拟合线性回归

加载样本数据。

load carsmall

将变量存储在表中。

tbl = table(Weight,Acceleration,MPG,'VariableNames',{'Weight','Acceleration','MPG'});

显示表的前五行。

tbl(1:5,:)

ans=5×3 table
    Weight    Acceleration    MPG
    ______    ____________    ___

     3504           12        18 
     3693         11.5        15 
     3436           11        18 
     3433           12        16 
     3449         10.5        17

拟合每加仑英里数 (MPG) 的线性回归模型。使用 Wilkinson 表示法指定模型公式。

lm = fitlm(tbl,'MPG~Weight+Acceleration')

lm = 
Linear regression model:
    MPG ~ 1 + Weight + Acceleration

Estimated Coefficients:
                     Estimate         SE         tStat       pValue  
                    __________    __________    _______    __________

    (Intercept)         45.155        3.4659     13.028    1.6266e-22
    Weight          -0.0082475    0.00059836    -13.783    5.3165e-24
    Acceleration       0.19694       0.14743     1.3359       0.18493


Number of observations: 94, Error degrees of freedom: 91
Root Mean Squared Error: 4.12
R-squared: 0.743,  Adjusted R-Squared: 0.738
F-statistic vs. constant model: 132, p-value = 1.38e-27

此示例中的 'MPG~Weight+Acceleration' 模型等效于将模型设定设置为 'linear'。例如，

lm2 = fitlm(tbl,'linear');

如果您对模型设定使用字符向量，但没有指定响应变量，则 fitlm 接受 tbl 中的最后一个变量作为响应变量，其他变量作为预测变量。

使用指定的模型公式拟合线性回归

使用由 Wilkinson 表示法指定的模型公式拟合线性回归模型。

加载样本数据。

load carsmall

将变量存储在表中。

tbl = table(Weight,Acceleration,Model_Year,MPG,'VariableNames',{'Weight','Acceleration','Model_Year','MPG'});

以权重和加速度为预测变量，拟合每加仑英里数 (MPG) 的线性回归模型。

lm = fitlm(tbl,'MPG~Weight+Acceleration')

lm = 
Linear regression model:
    MPG ~ 1 + Weight + Acceleration

Estimated Coefficients:
                     Estimate         SE         tStat       pValue  
                    __________    __________    _______    __________

    (Intercept)         45.155        3.4659     13.028    1.6266e-22
    Weight          -0.0082475    0.00059836    -13.783    5.3165e-24
    Acceleration       0.19694       0.14743     1.3359       0.18493


Number of observations: 94, Error degrees of freedom: 91
Root Mean Squared Error: 4.12
R-squared: 0.743,  Adjusted R-Squared: 0.738
F-statistic vs. constant model: 132, p-value = 1.38e-27

p 值 0.18493 表示 Acceleration 对 MPG 没有重大影响。

从模型中删除 Acceleration，并尝试通过添加预测变量 Model_Year 来改进模型。首先将 Model_Year 定义为分类变量。

tbl.Model_Year = categorical(tbl.Model_Year);
lm = fitlm(tbl,'MPG~Weight+Model_Year')

lm = 
Linear regression model:
    MPG ~ 1 + Weight + Model_Year

Estimated Coefficients:
                      Estimate         SE         tStat       pValue  
                     __________    __________    _______    __________

    (Intercept)           40.11        1.5418     26.016    1.2024e-43
    Weight           -0.0066475    0.00042802    -15.531    3.3639e-27
    Model_Year_76        1.9291       0.74761     2.5804      0.011488
    Model_Year_82        7.9093       0.84975     9.3078    7.8681e-15


Number of observations: 94, Error degrees of freedom: 90
Root Mean Squared Error: 2.92
R-squared: 0.873,  Adjusted R-Squared: 0.868
F-statistic vs. constant model: 206, p-value = 3.83e-40

使用 Wilkinson 表示法指定 modelspec 使您能够更新模型而无需更改设计矩阵。fitlm 仅使用在公式中指定的变量。它还为分类变量 Model_Year 创建两个必要的虚拟指示变量。

用项矩阵拟合线性回归

使用项矩阵拟合线性回归模型。

采用表输入时的项矩阵

如果模型变量在表中，则项矩阵中的 0 列表示响应变量的位置。

加载 hospital 数据集。

load hospital

将变量存储在表中。

t = table(hospital.Sex,hospital.BloodPressure(:,1),hospital.Age,hospital.Smoker, ...
    'VariableNames',{'Sex','BloodPressure','Age','Smoker'});

使用项矩阵表示线性模型 'BloodPressure ~ 1 + Sex + Age + Smoker'。响应变量位于表的第二列中，因此项矩阵的第二列必须是由 0 组成的列，以表示响应变量。

T = [0 0 0 0;1 0 0 0;0 0 1 0;0 0 0 1]

T = 4×4

     0     0     0     0
     1     0     0     0
     0     0     1     0
     0     0     0     1

拟合线性模型。

mdl1 = fitlm(t,T)

mdl1 = 
Linear regression model:
    BloodPressure ~ 1 + Sex + Age + Smoker

Estimated Coefficients:
                   Estimate       SE        tStat        pValue  
                   ________    ________    ________    __________

    (Intercept)      116.14      2.6107      44.485    7.1287e-66
    Sex_Male       0.050106     0.98364    0.050939       0.95948
    Age            0.085276    0.066945      1.2738        0.2058
    Smoker_1           9.87      1.0346      9.5395    1.4516e-15


Number of observations: 100, Error degrees of freedom: 96
Root Mean Squared Error: 4.78
R-squared: 0.507,  Adjusted R-Squared: 0.492
F-statistic vs. constant model: 33, p-value = 9.91e-15

采用矩阵输入时的项矩阵

如果预测变量和响应变量包含在矩阵和列向量中，则必须在项矩阵每一行的末尾包含 0，以表示响应变量。

加载 carsmall 数据集，并定义预测变量矩阵。

load carsmall
X = [Acceleration,Weight];

使用项矩阵指定模型 'MPG ~ Acceleration + Weight + Acceleration:Weight + Weight^2'。此模型包括变量 Acceleration 和 Weight 的主效应和双向交互效应项，以及变量 Weight 的二阶项。

T = [0 0 0;1 0 0;0 1 0;1 1 0;0 2 0]

T = 5×3

     0     0     0
     1     0     0
     0     1     0
     1     1     0
     0     2     0

拟合线性模型。

mdl2 = fitlm(X,MPG,T)

mdl2 = 
Linear regression model:
    y ~ 1 + x1*x2 + x2^2

Estimated Coefficients:
                    Estimate          SE         tStat       pValue  
                   ___________    __________    _______    __________

    (Intercept)         48.906        12.589     3.8847    0.00019665
    x1                 0.54418       0.57125    0.95261       0.34337
    x2               -0.012781     0.0060312    -2.1192      0.036857
    x1:x2          -0.00010892    0.00017925    -0.6076         0.545
    x2^2            9.7518e-07    7.5389e-07     1.2935       0.19917


Number of observations: 94, Error degrees of freedom: 89
Root Mean Squared Error: 4.1
R-squared: 0.751,  Adjusted R-Squared: 0.739
F-statistic vs. constant model: 67, p-value = 4.99e-26

只有截距和 x2 项（对应于 Weight 变量）在 5% 显著性水平上是显著的。

具有分类预测变量的线性回归

拟合包含分类预测变量的线性回归模型。对分类预测变量的类别重新排序，以控制模型中的参考水平。然后，使用 anova 检验分类变量的显著性。

具有分类预测变量的模型

加载 carsmall 数据集，并创建 MPG 的线性回归模型作为 Model_Year 的函数。要将数值向量 Model_Year 视为分类变量，请使用 'CategoricalVars' 名称-值对组参数标识预测变量。

load carsmall
mdl = fitlm(Model_Year,MPG,'CategoricalVars',1,'VarNames',{'Model_Year','MPG'})

mdl = 
Linear regression model:
    MPG ~ 1 + Model_Year

Estimated Coefficients:
                     Estimate      SE      tStat       pValue  
                     ________    ______    ______    __________

    (Intercept)        17.69     1.0328    17.127    3.2371e-30
    Model_Year_76     3.8839     1.4059    2.7625     0.0069402
    Model_Year_82      14.02     1.4369    9.7571    8.2164e-16


Number of observations: 94, Error degrees of freedom: 91
Root Mean Squared Error: 5.56
R-squared: 0.531,  Adjusted R-Squared: 0.521
F-statistic vs. constant model: 51.6, p-value = 1.07e-15

显示信息的模型公式 MPG ~ 1 + Model_Year 对应于

$MPG = β_{0} + β_{1} Ι_{Year = 76} + β_{2} Ι_{Year = 82} + ϵ$ ,

其中， $Ι_{Year = 76}$ 和 $Ι_{Year = 82}$ 是指示变量，如果 Model_Year 的值分别为 76 和 82，则其值为 1。Model_Year 变量包含三个不同值，您可以使用 unique 函数来进行检查。

unique(Model_Year)

fitlm 选择 Model_Year 中的最小值作为参考水平 ('70')，并创建两个指示变量 $Ι_{Year = 76}$ 和 $Ι_{Year = 82}$ 。该模型仅包括两个指示变量，因为如果该模型包括三个指示变量（每个水平一个）和一个截距项，则设计矩阵变为秩亏矩阵。

具有全指示变量的模型

您可以将 mdl 的模型公式解释为一个具有三个指示变量而没有截距项的模型：

$y = β_{0} Ι_{x_{1} = 70} + (β_{0} + β_{1}) Ι_{x_{1} = 76} + ({β_{0} + β}_{2}) Ι_{x_{2} = 82} + ϵ$ .

您也可以通过手动创建指示变量并指定模型公式，创建包含三个指示变量而没有截距项的模型。

temp_Year = dummyvar(categorical(Model_Year));
Model_Year_70 = temp_Year(:,1);
Model_Year_76 = temp_Year(:,2);
Model_Year_82 = temp_Year(:,3);
tbl = table(Model_Year_70,Model_Year_76,Model_Year_82,MPG);
mdl = fitlm(tbl,'MPG ~ Model_Year_70 + Model_Year_76 + Model_Year_82 - 1')

mdl = 
Linear regression model:
    MPG ~ Model_Year_70 + Model_Year_76 + Model_Year_82

Estimated Coefficients:
                     Estimate      SE       tStat       pValue  
                     ________    _______    ______    __________

    Model_Year_70      17.69      1.0328    17.127    3.2371e-30
    Model_Year_76     21.574     0.95387    22.617    4.0156e-39
    Model_Year_82      31.71     0.99896    31.743    5.2234e-51


Number of observations: 94, Error degrees of freedom: 91
Root Mean Squared Error: 5.56

选择模型中的参考水平

您可以通过修改分类变量中类别的顺序来选择参考水平。首先，创建一个分类变量 Year。

Year = categorical(Model_Year);

使用 categories 函数检查类别的顺序。

categories(Year)

ans = 3x1 cell
    {'70'}
    {'76'}
    {'82'}

如果您使用 Year 作为预测变量，则 fitlm 选择第一个类别 '70' 作为参考水平。使用 reordercats 函数对 Year 重新排序。

Year_reordered = reordercats(Year,{'76','70','82'});
categories(Year_reordered)

ans = 3x1 cell
    {'76'}
    {'70'}
    {'82'}

Year_reordered 的第一个类别是 '76'。创建 MPG 为 Year_reordered 的函数的线性回归模型。

mdl2 = fitlm(Year_reordered,MPG,'VarNames',{'Model_Year','MPG'})

mdl2 = 
Linear regression model:
    MPG ~ 1 + Model_Year

Estimated Coefficients:
                     Estimate      SE        tStat       pValue  
                     ________    _______    _______    __________

    (Intercept)       21.574     0.95387     22.617    4.0156e-39
    Model_Year_70    -3.8839      1.4059    -2.7625     0.0069402
    Model_Year_82     10.136      1.3812     7.3385    8.7634e-11


Number of observations: 94, Error degrees of freedom: 91
Root Mean Squared Error: 5.56
R-squared: 0.531,  Adjusted R-Squared: 0.521
F-statistic vs. constant model: 51.6, p-value = 1.07e-15

mdl2 使用 '76' 作为参考水平，并包括两个指示变量 $Ι_{Year = 70}$ 和 $Ι_{Year = 82}$ 。

计算分类预测变量

mdl2 的模型显示包括每个项的 p 值，以检验对应的系数是否等于零。每个 p 值检查每个指示变量。要将分类变量 Model_Year 作为一组指示变量进行检查，请使用 anova。使用 'components'（默认值）选项返回成分 ANOVA 表，该表包含模型中除常数项之外的每个变量的 ANOVA 统计量。

anova(mdl2,'components')

ans=2×5 table
                  SumSq     DF    MeanSq      F        pValue  
                  ______    __    ______    _____    __________

    Model_Year    3190.1     2    1595.1    51.56    1.0694e-15
    Error         2815.2    91    30.936

成分 ANOVA 表包括 Model_Year 变量的 p 值，该值小于指示变量的 p 值。

为线性模型指定响应变量和预测变量

对样本数据进行线性回归模型拟合。指定响应变量和预测变量，并且在模型中仅包括成对的交互效应项。

加载样本数据。

load hospital

对数据进行具有交互效应项的线性模型拟合。指定体重作为响应变量，性别、年龄和吸烟状况作为预测变量。此外，指定性别和吸烟状况是分类变量。

mdl = fitlm(hospital,'interactions','ResponseVar','Weight',...
    'PredictorVars',{'Sex','Age','Smoker'},...
    'CategoricalVar',{'Sex','Smoker'})

mdl = 
Linear regression model:
    Weight ~ 1 + Sex*Age + Sex*Smoker + Age*Smoker

Estimated Coefficients:
                         Estimate      SE        tStat        pValue  
                         ________    _______    ________    __________

    (Intercept)             118.7     7.0718      16.785     6.821e-30
    Sex_Male               68.336     9.7153      7.0339    3.3386e-10
    Age                   0.31068    0.18531      1.6765      0.096991
    Smoker_1               3.0425     10.446     0.29127       0.77149
    Sex_Male:Age         -0.49094    0.24764     -1.9825      0.050377
    Sex_Male:Smoker_1      0.9509     3.8031     0.25003       0.80312
    Age:Smoker_1         -0.07288    0.26275    -0.27737       0.78211


Number of observations: 100, Error degrees of freedom: 93
Root Mean Squared Error: 8.75
R-squared: 0.898,  Adjusted R-Squared: 0.892
F-statistic vs. constant model: 137, p-value = 6.91e-44

根据年龄、吸烟状况或这些因子与患者性别在 5% 显著性水平上的交互效应，患者的体重似乎没有显著差异。

拟合稳健线性回归模型

加载 hald 数据集，该数据集测量水泥成分对其硬化热的影响。

load hald

该数据集包括变量 ingredients 和 heat。矩阵 ingredients 包含水泥中四种化学成分的百分比组成。向量 heat 包含每个水泥样本在 180 天后的热硬化值。

对数据进行稳健线性回归模型拟合。

mdl = fitlm(ingredients,heat,'RobustOpts','on')

mdl = 
Linear regression model (robust fit):
    y ~ 1 + x1 + x2 + x3 + x4

Estimated Coefficients:
                   Estimate      SE        tStat       pValue 
                   ________    _______    ________    ________

    (Intercept)       60.09     75.818     0.79256      0.4509
    x1               1.5753    0.80585      1.9548    0.086346
    x2               0.5322    0.78315     0.67957     0.51596
    x3              0.13346     0.8166     0.16343     0.87424
    x4             -0.12052     0.7672    -0.15709     0.87906


Number of observations: 13, Error degrees of freedom: 8
Root Mean Squared Error: 2.65
R-squared: 0.979,  Adjusted R-Squared: 0.969
F-statistic vs. constant model: 94.6, p-value = 9.03e-07

有关详细信息，请参阅主题Reduce Outlier Effects Using Robust Regression，该主题将稳健拟合的结果与标准最小二乘拟合进行比较。

使用交叉验证计算均值绝对误差

使用 10 折交叉验证计算回归模型的均值绝对误差。

加载 carsmall 数据集。将 Acceleration 和 Displacement 变量指定为预测变量，将 Weight 变量指定为响应变量。

load carsmall
X1 = Acceleration;
X2 = Displacement;
y = Weight;

创建自定义函数 regf（如此示例末尾所示）。此函数将回归模型与训练数据进行拟合，然后基于测试集计算预测的汽车重量。该函数将预测的汽车重量值与实际值进行比较，然后计算均值绝对误差 (MAE) 和根据测试集汽车重量范围调整的 MAE。

注意：如果使用此示例的实时脚本文件，则文件末尾已包含 regf 函数。否则，您需要在 .m 文件的末尾创建此函数，或将其作为文件添加到 MATLAB® 路径中。

默认情况下，crossval 执行 10 折交叉验证。对于 X1、X2 和 y 中数据的 10 个训练和测试集分区，使用 regf 函数计算 MAE 和调整后的 MAE 值。求 MAE 均值和调整后的 MAE 均值。

rng('default') % For reproducibility
values = crossval(@regf,X1,X2,y)

values = 10×2

  319.2261    0.1132
  342.3722    0.1240
  214.3735    0.0902
  174.7247    0.1128
  189.4835    0.0832
  249.4359    0.1003
  194.4210    0.0845
  348.7437    0.1700
  283.1761    0.1187
  210.7444    0.1325

mean(values)

ans = 1×2

  252.6701    0.1129

以下代码创建函数 regf。

function errors = regf(X1train,X2train,ytrain,X1test,X2test,ytest)
tbltrain = table(X1train,X2train,ytrain, ...
    'VariableNames',{'Acceleration','Displacement','Weight'});
tbltest = table(X1test,X2test,ytest, ...
    'VariableNames',{'Acceleration','Displacement','Weight'});
mdl = fitlm(tbltrain,'Weight ~ Acceleration + Displacement');
yfit = predict(mdl,tbltest);
MAE = mean(abs(yfit-tbltest.Weight));
adjMAE = MAE/range(tbltest.Weight);
errors = [MAE adjMAE];
end

输入参数

`tbl` — 输入数据
表 | 数据集数组

输入数据，包括预测变量和响应变量，指定为表或数据集数组。预测变量可以是数值、逻辑值、分类、字符或字符串。响应变量必须为数值或逻辑值。

默认情况下，fitlm 将最后一个变量作为响应变量，其他变量作为预测变量。
要将另外的列设置为响应变量，请使用 ResponseVar 名称-值对组参数。
要使用列的子集作为预测变量，请使用 PredictorVars 名称-值对组参数。
要定义模型设定，请使用公式或项矩阵设置 modelspec 参数。公式或项矩阵指定哪些列用作预测变量或响应变量。

表中的变量名称不必是有效的 MATLAB^® 标识符，但名称不能包含前导空格或尾部空格。如果名称无效，则在拟合或调整模型时无法使用公式；例如：

您无法使用公式指定 modelspec。
当您分别使用 addTerms 函数或 removeTerms 函数时，无法使用公式指定要添加或删除的项。
当您使用带名称-值对组参数 'Lower' 和 'Upper' 的 step 或 stepwiselm 函数时，则无法使用公式来指定模型的下界和上界。

您可以使用 isvarname 函数来验证 tbl 中的变量名称。如果变量名称无效，可以使用 matlab.lang.makeValidName 函数进行转换。

`X` — 预测变量
矩阵

预测变量，指定为 n×p 矩阵，其中 n 是观测值数目，p 是预测变量的数目。X 的每列表示一个变量，每行表示一个观测值。

默认情况下，模型中有一个常数项，除非您显式删除它，否则不要在 X 中包含由 1 组成的列。

数据类型： single | double

`y` — 响应变量
向量

响应变量，指定为 n×1 向量，其中 n 是观测值数目。y 中的每个条目是对 X 的对应行的响应。

数据类型： single | double | logical

`modelspec` — 模型设定
`'linear'` （默认） | 命名模型的字符向量或字符串标量 | t×(p + 1) 项矩阵 | `'y ~ terms'` 形式的字符向量或字符串标量公式

模型设定，指定为下列值之一。

命名模型的字符向量或字符串标量。

值	模型类型
`'constant'`	模型只包含一个常数（截距）项。
`'linear'`	模型包含每个预测变量的截距和线性项。
`'interactions'`	模型包含每个预测变量的截距、线性项以及不同预测变量对的所有乘积（无平方项）。
`'purequadratic'`	模型包含每个预测变量的截距项、线性项和平方项。
`'quadratic'`	模型包含截每个预测变量的截距项、线性项和平方项，以及不同预测变量对组的所有乘积。
`'polyijk'`	模型是一个多项式，其中具有第一个预测变量的 1 到 `i` 次的所有项，第二个预测变量的 1 到 `j` 次的所有项，依此类推。请使用数字 0 到 9 指定每个预测变量的最大次数。模型包含交互效应项，但是，每个交互效应项的次数不超过指定次数的最大值。例如，`'poly13'` 具有截距和 x₁、x₂、x₂²、x₂³、x₁x₂ 和 x₁x₂² 项，其中 x₁ 和 x₂ 分别是第一个和第二个预测变量。

t×(p + 1) 矩阵或项矩阵，指定模型中的项，其中 t 是项数，p 是预测变量数，而 + 1 表示响应变量。当预测变量的数目很大并且您要以编程方式生成项时，项矩阵是很方便的。
如下形式的字符向量或字符串标量公式：

'y ~ terms',
其中 terms 位于Wilkinson 表示法中。公式中的变量名称必须为 tbl 中的变量名称或由 Varnames 指定的变量名称。此外，变量名称必须为有效的 MATLAB 标识符。
软件使用 tbl 或 X 中各项的顺序来确定拟合模型中各项的顺序。因此，模型中各项的顺序可能不同于指定公式中各项的顺序。

示例： 'quadratic'

示例： 'y ~ x1 + x2^2 + x1:x2'

数据类型： single | double | char | string

名称-值参数

将可选的参数对组指定为 Name1=Value1,...,NameN=ValueN，其中 Name 是参数名称，Value 是对应的值。名称-值参数必须出现在其他参数后，但参数对组的顺序无关紧要。

在 R2021a 之前，使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例： 'Intercept',false,'PredictorVars',[1,3],'ResponseVar',5,'RobustOpts','logistic' 指定没有常数项的稳健回归模型，其中算法使用带默认调整常量的逻辑加权函数，第一个和第三个变量是预测变量，第五个变量是响应变量。

`CategoricalVars` — 分类变量列表
字符串数组 | 字符向量元胞数组 | 逻辑或数值索引向量

分类变量列表，指定为以逗号分隔的对组，其中包含 'CategoricalVars' 和字符串数组或字符向量元胞数组（包含表或数据集数组 tbl 中分类变量的名称）或者逻辑或数值索引向量（指示哪些列是分类变量）。

如果数据在表或数据集数组 tbl 中，则默认情况下，fitlm 将所有分类值、逻辑值、字符数组、字符串数组和字符向量元胞数组视为分类变量。
如果数据在矩阵 X 中，则 'CategoricalVars' 的默认值为空矩阵 []。也就是说，除非您将变量指定为分类变量，否则默认视为非分类变量。

例如，您可以使用以下任一选项将六个变量中的第二个和第三个指定为分类变量：

示例： 'CategoricalVars',[2,3]

示例： 'CategoricalVars',logical([0 1 1 0 0 0])

数据类型： single | double | logical | string | cell

`Exclude` — 要排除的观测值
逻辑或数值索引向量

要从拟合中排除的观测值，指定为以逗号分隔的对组，其中包含 'Exclude' 和逻辑或数值索引向量，指示要从拟合中排除哪些观测值。

例如，您可以使用以下任一示例排除 6 个观测值中的 2 个和 3 个。

示例： 'Exclude',[2,3]

示例： 'Exclude',logical([0 1 1 0 0 0])

数据类型： single | double | logical

`Intercept` — 常数项的指示符
`true` （默认） | `false`

拟合中常数项（截距）的指示符，指定为以逗号分隔的对组，其中包含 'Intercept' 以及 true（表示在模型中包含常数项）或 false（表示从模型中删除常数项）。

仅当使用字符向量或字符串标量而不是公式或矩阵指定模型时，才使用 'Intercept'。

示例： 'Intercept',false

`PredictorVars` — 预测变量
字符串数组 | 字符向量元胞数组 | 逻辑或数值索引向量

拟合中要使用的预测变量，指定为以逗号分隔的对组，其中包含 'PredictorVars' 和字符串数组或字符向量元胞数组（包含表或数据集数组包含 tbl 中变量名称），或是逻辑或数值索引向量（指示哪些列是预测变量）。

字符串值或字符向量应为 tbl 中的名称，或在您使用 'VarNames' 名称-值对组参数指定的名称。

默认值为 X 中的所有变量，或 tbl 中除 ResponseVar 以外的所有变量。

例如，您可以使用以下任一示例将第二个和第三个变量指定为预测变量。

示例： 'PredictorVars',[2,3]

示例： 'PredictorVars',logical([0 1 1 0 0 0])

数据类型： single | double | logical | string | cell

`ResponseVar` — 响应变量
`tbl` 中的最后一列（默认） | 包含变量名称的字符向量或字符串标量 | 逻辑或数值索引向量

拟合中要使用的响应变量，指定为以逗号分隔的对组，其中包含 'ResponseVar' 和字符向量或字符串标量（包含表或数据集数组 tbl 中变量的名称），或者逻辑或数值索引向量（指示哪个列是响应变量）。在拟合表或数据集数组 tbl 时，通常需要使用 'ResponseVar'。

例如，您可以通过以下方式之一指定第四个变量 yield 作为六个变量的响应。

示例： 'ResponseVar','yield'

示例： 'ResponseVar',[4]

示例： 'ResponseVar',logical([0 0 0 1 0 0])

数据类型： single | double | logical | char | string

`RobustOpts` — 稳健拟合类型的指示符
`'off'` （默认） | `'on'` | 字符向量 | 字符串标量 | 结构体

要使用的稳健拟合类型的指示符，指定为以逗号分隔的对组，其中包含 'RobustOpts' 和下列值之一。

'off' - 没有稳健拟合。fitlm 使用普通最小二乘法。
'on' - 使用具有默认调整常量的 'bisquare' 权重函数进行稳健拟合。
字符向量或字符串标量 - 下表中稳健拟合权重函数的名称。fitlm 使用表中指定的对应默认调整常量。

包含两个字段 RobustWgtFun 和 Tune 的结构体。

RobustWgtFun 字段包含下表中稳健拟合权重函数的名称或自定义权重函数的函数句柄。
Tune 字段包含调整常量。如果未设置 Tune 字段，fitlm 将使用对应的默认调整常量。

权重函数	描述	默认调整常量
`'andrews'`	`w = (abs(r)<pi) .* sin(r) ./ r`	1.339
`'bisquare'`	`w = (abs(r)<1) .* (1 - r.^2).^2`（也称为双权）	4.685
`'cauchy'`	`w = 1 ./ (1 + r.^2)`	2.385
`'fair'`	`w = 1 ./ (1 + abs(r))`	1.400
`'huber'`	`w = 1 ./ max(1, abs(r))`	1.345
`'logistic'`	`w = tanh(r) ./ r`	1.205
`'ols'`	普通最小二乘法（无加权函数）	无
`'talwar'`	`w = 1 * (abs(r)<1)`	2.795
`'welsch'`	`w = exp(-(r.^2))`	2.985
函数句柄	自定义权重函数，接受缩放残差的向量 `r`，并返回与 `r` 大小相同的权重向量	1

使用内置权重函数的默认调整常量得到的系数估计值的统计效率是普通最小二乘估计值的 95%，前提是响应具无离群值的正态分布。降低调整常量会增加分配给大残差的降权；增加调整常量会降低分配给大残差的降权。
权重函数中的值 r 为
r = resid/(tune*s*sqrt(1–h)),
其中，resid 是上一次迭代的残差向量，tune 是调整常量，h 是最小二乘拟合的杠杆值向量，s 是误差项的标准差的估计值，由下式给出
s = MAD/0.6745.
MAD 是残差与其中位数的中位数绝对偏差。常量 0.6745 使正态分布的估计无偏。如果 X 有 p 个列，软件在计算中位数时会排除最小的 p 个绝对偏差。

对于稳健拟合，fitlm 使用 M 估计来构成估计方程，并使用 Iteratively Reweighted Least Squares (IRLS) 方法求解它们。

示例： 'RobustOpts','andrews'

`VarNames` — 变量的名称
`{'x1','x2',...,'xn','y'}` （默认） | 字符串数组 | 字符向量元胞数组

变量的名称，指定为以逗号分隔的对组，其中前面包含 'VarNames' 和字符串数组或字符向量元胞数组（包含 X 列的名称），最后包含响应变量 y 的名称。

'VarNames' 不适用于表或数据集数组中的变量，因为这些变量已有名称。

变量名称不必是有效的 MATLAB 标识符，但名称不能包含前导空格或尾部空格。如果名称无效，则在拟合或调整模型时无法使用公式；例如：

当您分别使用 addTerms 函数或 removeTerms 函数时，无法使用公式指定要添加或删除的项。
当您使用带名称-值对组参数 'Lower' 和 'Upper' 的 step 或 stepwiselm 函数时，则无法使用公式来指定模型的下界和上界。

在指定 'VarNames',varNames 之前，您可以使用 isvarname 函数验证 varNames 中的变量名称。如果变量名称无效，可以使用 matlab.lang.makeValidName 函数进行转换。

示例： 'VarNames',{'Horsepower','Acceleration','Model_Year','MPG'}

数据类型： string | cell

`Weights` — 观测值权重
`ones(n,1)` （默认） | 非负标量值的 n×1 向量

观测值权重，指定为以逗号分隔的对组，其中包含 'Weights' 和非负标量值的 n×1 向量，其中 n 是观测值数目。

数据类型： single | double

输出参数

`mdl` — 线性模型
`LinearModel` 对象

表示对数据响应的最小二乘拟合的线性模型，以 LinearModel 对象形式返回。

如果 'RobustOpts' 名称-值对组的值不是 [] 或 'ols'，则模型不是最小二乘拟合，而是使用稳健拟合函数。

详细信息