gallery
测试矩阵
语法
说明
[ 生成由 A1,A2,...,Am] = gallery(matrixname,P1,P2,...,Pn)matrixname 指定的一系列测试矩阵。P1,P2,...,Pn 是单个矩阵系列要求的输入参数。调用语法中使用的输入参数 P1,P2,...,Pn 的数目因矩阵而异。matrixname 一节中说明了每个矩阵系列的确切调用语法。
[ 还指定生成的测试矩阵的数据类型。A1,A2,...,Am] = gallery(matrixname,P1,P2,...,Pn,typename)
示例
以缩放颜色显示几个测试矩阵的矩阵元素。
创建一个大小为 11×11 的循环矩阵。循环矩阵是一种特殊的托普利茨矩阵,其中每行都通过周期性地将上一行中的各元向右移一位来获得。
C = gallery("circul",11); 显示 C 中矩阵元素的图像。向图形添加颜色栏以显示当前颜色图。
imagesc(C)
axis square
colorbar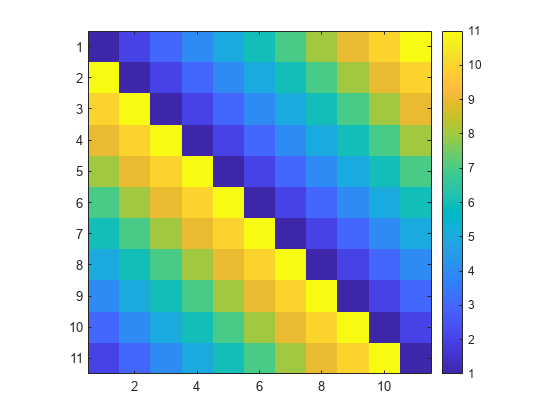
创建一个大小为 11×11 的 grcar 矩阵。grcar 矩阵是一种非对称的托普利茨矩阵,其下对角线上的元素为 -1,主对角线上的元素为 1,主对角线上方的少数几个对角线上的元素为 1。
G = gallery("grcar",11); 显示 G 中矩阵元素的图像。
imagesc(G)
axis square
colorbar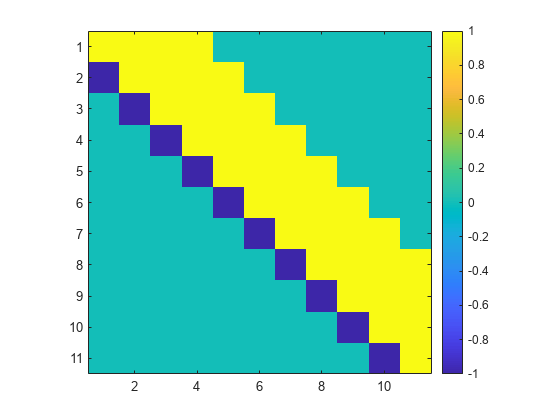
创建一个大小为 11×11 的 minij 矩阵。minij 矩阵 M 是一种其元素满足 M(i,j) = min(i,j) 的对称正定矩阵。
M = gallery("minij",11); 显示 M 中矩阵元素的图像。
imagesc(M)
axis square
colorbar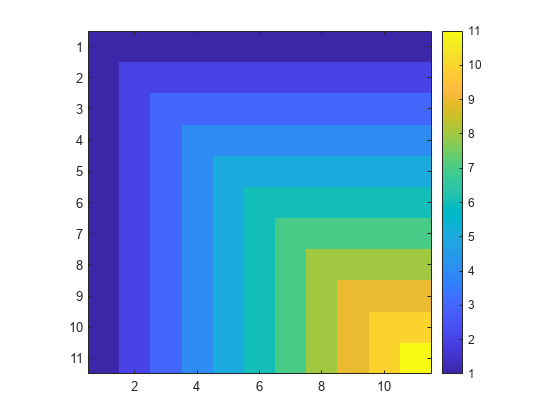
当且仅当整数矩阵的行列式正好是 1 或 –1 时,其逆矩阵也是整数矩阵。行列式为 1 或 –1 的整数方阵也称为幺模矩阵。例如,gallery("dramadah",n) 就是这样一种矩阵,它是由 0 和 1 组成的 n×n 矩阵,行列式为 1 或 –1。
创建一个 6×6 的 dramadah 矩阵。计算其行列式和逆矩阵。
A = gallery("dramadah",6)A = 6×6
1 1 0 1 0 0
0 1 1 0 1 0
0 0 1 1 0 1
1 0 0 1 1 0
1 1 0 0 1 1
0 1 1 0 0 1
detA = det(A)
detA = -1
invA = inv(A)
invA = 6×6
-1 -2 -3 4 -2 5
1 1 1 -2 1 -2
-1 -1 -2 3 -2 4
1 1 2 -2 1 -3
0 1 1 -1 1 -2
0 0 1 -1 1 -1
该矩阵的逆矩阵只包含整数项,因为原始矩阵的行列式是 -1。
此示例说明如何使用 Householder 变换来计算矩阵 的 QR 分解,其中 是正交矩阵, 是上三角矩阵。
首先,将随机数生成器设置为默认值,并创建由服从标准正态分布的随机数组成的 6×3 矩形矩阵。
rng("default")
A = randn(6,3)A = 6×3
0.5377 -0.4336 0.7254
1.8339 0.3426 -0.0631
-2.2588 3.5784 0.7147
0.8622 2.7694 -0.2050
0.3188 -1.3499 -0.1241
-1.3077 3.0349 1.4897
要创建 Householder 矩阵,请使用函数 [v,beta] = gallery("house",x)。该函数采用列向量 ,并返回 和 ,满足 即获得 Householder 矩阵。Householder 变换用于将除了向量 的第一个元素之外的所有元素归零。
计算 Householder 矩阵 并执行变换 。矩阵 在第一列的对角线下只包含零。
[v1,beta1] = gallery("house",A(:,1));
P1 = eye(6) - beta1*(v1*v1');
A1 = P1*AA1 = 6×3
-3.3630 2.8841 1.0421
0.0000 1.9024 0.0858
-0.0000 1.6571 0.5314
0.0000 3.5028 -0.1350
0.0000 -1.0788 -0.0983
0 1.9227 1.3835
接下来,计算 Householder 矩阵 ,使得 在第一列和第二列中的对角线下只包含零。
[v2,beta2] = gallery("house",A1(2:end,2));
v2 = [0;v2];
P2 = eye(6) - beta2*(v2*v2');
A2 = P2*A1A2 = 6×3
-3.3630 2.8841 1.0421
-0.0000 -4.8472 -0.6885
-0.0000 0.0000 0.3413
-0.0000 0.0000 -0.5368
0.0000 -0.0000 0.0255
-0.0000 0.0000 1.1630
最后,计算 Householder 矩阵 ,使得 下对角线元素全部为零。
[v3,beta3] = gallery("house",A2(3:end,3));
v3 = [0;0;v3];
P3 = eye(6) - beta3*(v3*v3');
R = P3*A2R = 6×3
-3.3630 2.8841 1.0421
-0.0000 -4.8472 -0.6885
0.0000 -0.0000 -1.3258
-0.0000 0.0000 0.0000
0.0000 -0.0000 -0.0000
0.0000 0.0000 -0.0000
矩阵 是上三角矩阵。由于 Householder 矩阵是对合矩阵(矩阵与其逆矩阵相同), 的 QR 分解成为 和 。
Q = P1*P2*P3
Q = 6×6
-0.1599 -0.0057 -0.6699 0.4983 -0.2036 -0.4857
-0.5453 -0.3952 -0.1759 -0.6432 0.1342 -0.2895
0.6717 -0.3386 0.1647 -0.0991 0.1551 -0.6109
-0.2564 -0.7239 0.3290 0.5244 0.0805 0.1434
-0.0948 0.2221 -0.0962 0.1872 0.9463 -0.0433
0.3888 -0.3948 -0.6130 -0.1346 0.1203 0.5335
将此结果与使用 qr 函数的计算结果进行比较。
[Qa,Ra] = qr(A)
Qa = 6×6
-0.1599 -0.0057 -0.6699 0.4983 -0.2036 -0.4857
-0.5453 -0.3952 -0.1759 -0.6432 0.1342 -0.2895
0.6717 -0.3386 0.1647 -0.0991 0.1551 -0.6109
-0.2564 -0.7239 0.3290 0.5244 0.0805 0.1434
-0.0948 0.2221 -0.0962 0.1872 0.9463 -0.0433
0.3888 -0.3948 -0.6130 -0.1346 0.1203 0.5335
Ra = 6×3
-3.3630 2.8841 1.0421
0 -4.8472 -0.6885
0 0 -1.3258
0 0 0
0 0 0
0 0 0
在计算机精度范围内验证 。
norm(A - Q*R)
ans = 4.7172e-15
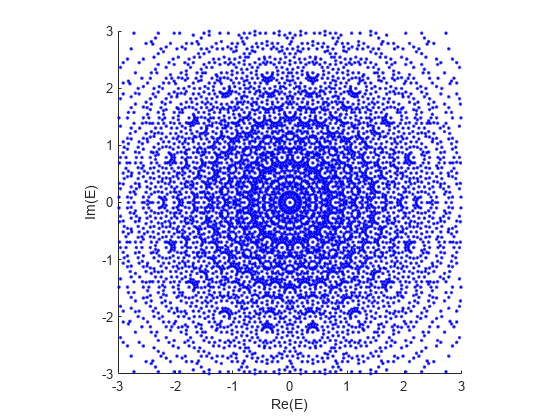
此示例绘制复平面上 20000 个大小为 18×18 的随机循环矩阵采样的特征值分布。矩阵元素从集合 {–0.4,0.4} 中均匀采样。
创建一个大小为 18×20000 的数组 E 来存储特征值。
E = zeros(18,20000);
将随机数生成器设置为默认值。在一个 for 循环语句中对以下操作迭代执行 20000 次:
创建一个 1×18 行向量
x,其中包含的随机元素为 –0.4 或 0.4。使用向量
x作为输入,创建随机循环矩阵A。找出
A的特征值,并将其存储在E中。
rng("default") for i = 1:20000 x = -0.4 + 0.8*randi([0 1],1,18); A = gallery("circul",x); E(:,i) = eig(A); end
创建一个散点图,以在复平面上显示特征值 E。将 和 轴范围设置为 –3 至 3。
scatter(real(E(:)),imag(E(:)),"b.") xlabel("Re(E)") ylabel("Im(E)") xlim([-3 3]) ylim([-3 3]) axis square
创建测试矩阵 gallery(3)。测试矩阵是病态矩阵,包含对扰动敏感的特征值。
A = gallery(3)
A = 3×3
-149 -50 -154
537 180 546
-27 -9 -25
使用 eig 计算 A 的特征值。
e = eig(A)
e = 3×1
1.0000
2.0000
3.0000
使用 condeig 计算特征值条件数。
c = condeig(A)
c = 3×1
603.6390
395.2366
219.2920
条件数表明,A 的矩阵元素中的扰动可导致其特征值的扰动,其上界约为 200 至 600 倍。
接下来,通过与一个由均匀分布的随机数组成的矩阵相加对 A 进行细微扰动。将随机数生成器的种子设置为其默认值。将 A 与一个随机矩阵相加,该矩阵中的元素在 0 到 0.001(不包含两者)的区间内。
rng("default")
Ap = A + 1e-3*rand(3)Ap = 3×3
-148.9992 -49.9991 -153.9997
537.0009 180.0006 546.0005
-26.9999 -8.9999 -24.9990
计算扰动矩阵 Ap 的特征值。
ep = eig(Ap)
ep = 3×1
0.7399
2.1437
3.1188
显示扰动特征值和原始特征值之间的差异。
delta = ep - e
delta = 3×1
-0.2601
0.1437
0.1188
将特征值的变化与特征值条件数提供的上界进行比较。上界与特征值扰动的数量级大致相同。
delta_upper = 1e-3*c
delta_upper = 3×1
0.6036
0.3952
0.2193
创建测试矩阵 A = gallery(5)。测试矩阵具有对舍入误差敏感的特征值。
A = gallery(5)
A = 5×5
-9 11 -21 63 -252
70 -69 141 -421 1684
-575 575 -1149 3451 -13801
3891 -3891 7782 -23345 93365
1024 -1024 2048 -6144 24572
在精确算术运算中,矩阵 A 具有 的五重特征值(严格地说,A 具有代数重数为 5 和几何重数为 1 的特征值 0)。这意味着 A 的精确特征多项式是 。验证 A^5 是零矩阵。
Afifth = A^5
Afifth = 5×5
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
将这些结果与使用 eig 的特征值的数值计算进行比较。eig 函数返回 A 的五个小特征值。
e = eig(A)
e = 5×1 complex
-0.0370 + 0.0275i
-0.0370 - 0.0275i
0.0147 + 0.0427i
0.0147 - 0.0427i
0.0445 + 0.0000i
这表明 A 的特征值的数值计算对舍入误差极为敏感,因为计算中使用了浮点精度。
特征值的数值计算与精确算术运算中的数值计算有很大不同。eig 函数并不求与 A 的精确特征值接近的特征值,而是求与 A 接近的矩阵的特征值。为了说明这一点,我们在复平面上绘制 A 的精确特征值和数值特征值。
plot(0,0,"bo",real(e),imag(e),"r*") axis([-0.1 0.1 -0.1 0.1]) axis square
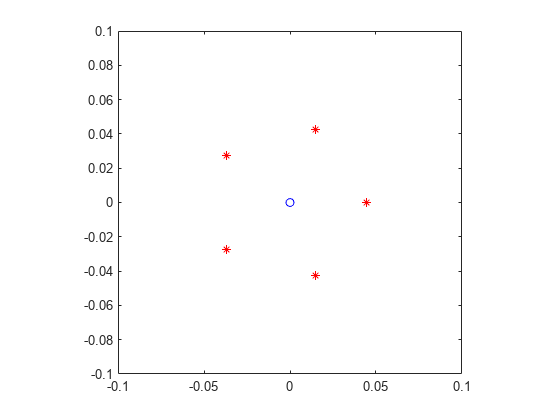
该图显示,数值特征值位于复平面中一个以原点为中心的正五边形的顶点上。该五边形的半径大约是 0.04。
接下来,计算与 A 相近的 20 个矩阵的特征值。将随机数生成器设置为默认值,并通过将服从标准正态分布的随机数乘以 eps 来扰动 A。绘制 20 个扰动矩阵的数值特征值。
E = zeros(20,5); rng("default") for i = 1:20 E(i,:) = eig(A + eps*randn(5).*A); end plot(0,0,"bo",real(e),imag(e),"r*",real(E),imag(E),"k.") axis([-0.1 0.1 -0.1 0.1]) axis square
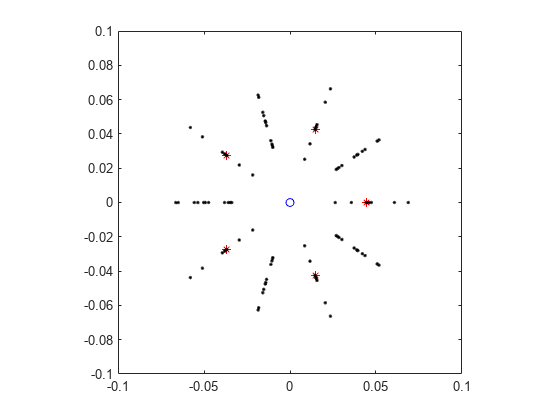
该图显示,当 A 受到扰动时,表示 A 的特征值的原始五边形可以翻转方向。20 个扰动矩阵的特征值位于半径在 0.01 到 0.07 范围内的五边形的顶点上。扰动矩阵的计算特征值的行为类似于原始矩阵的计算特征值。计算特征值的不准确性是由 gallery(5) 的敏感度造成的。
输入参数
矩阵系列的名称,指定为字符向量或字符串标量。参量 matrixname 决定生成的测试矩阵系列,如以下列表中所示。
| 描述:二项矩阵,它是对合矩阵的倍数 语法:
属性:
| ||||||||||||||||
| 描述:柯西矩阵 语法:
属性:
| ||||||||||||||||
| 描述:切比雪夫谱微分矩阵 语法:
属性:
| ||||||||||||||||
| 描述:切比雪夫多项式的类范德蒙类矩阵 语法:
| ||||||||||||||||
| 描述:奇异的托普利茨下黑森贝格矩阵 语法:
属性:
| ||||||||||||||||
| 描述:循环矩阵 语法:
属性:
另请参阅: | ||||||||||||||||
| 描述:具有零值对角线元的 Clement 三对角矩阵 语法:
属性:
| ||||||||||||||||
| 描述:比较矩阵 语法:
属性:
| ||||||||||||||||
| 描述:矩阵条件数估计量的反例 语法:
| ||||||||||||||||
| 描述:其列周期性重复的矩阵 语法:
| ||||||||||||||||
| 描述:对角占优、病态、三对角矩阵(稀疏矩阵) 语法:
| ||||||||||||||||
| 描述:由 0 和 1 组成的矩阵 语法:
| ||||||||||||||||
| 描述:费德勒对称矩阵 语法:
属性:
| ||||||||||||||||
| 描述:Forsythe 矩阵或扰动 Jordan 块 语法:
属性:
| ||||||||||||||||
| 描述:具有病态特征值的弗兰克矩阵 语法:
属性:
| ||||||||||||||||
| 描述:最大公约数矩阵 语法:
属性:
| ||||||||||||||||
| 描述:Gear 矩阵 语法:
属性:
| ||||||||||||||||
| 描述:具有敏感特征值的托普利茨矩阵 语法:
| ||||||||||||||||
| 描述:其特征值位于复平面中的垂直线上的矩阵 语法:
| ||||||||||||||||
| 描述:Householder 矩阵 语法:
| ||||||||||||||||
| 描述:由指定范围内均匀分布的随机采样整数组成的数组 语法:
| ||||||||||||||||
| 描述:上黑森贝格矩阵的逆矩阵 语法:
属性:
| ||||||||||||||||
| 描述:对合矩阵(矩阵与其逆矩阵相同) 语法:
属性:
另请参阅: | ||||||||||||||||
| 描述:含有阶乘元素的汉克尔矩阵 语法:
| ||||||||||||||||
| 描述:Jordan 分块矩阵 语法:
| ||||||||||||||||
| 描述:上梯形 Kahan 矩阵 语法:
| ||||||||||||||||
| 描述:Kac-Murdock-Szegö 托普利茨矩阵 语法:
属性:
| ||||||||||||||||
| 描述:克雷洛夫矩阵 语法:
| ||||||||||||||||
| 描述:Lauchli 矩形矩阵 语法:
属性:
| ||||||||||||||||
| 描述:Lehmer 对称正定矩阵 语法:
属性:
| ||||||||||||||||
| 描述:由 Leslie 人口模型的出生率和成活率组成的矩阵 语法:
| ||||||||||||||||
| 描述:含有实数敏感特征值的三对角矩阵 语法:
属性:
| ||||||||||||||||
| 描述:Lotkin 矩阵 语法:
属性:
| ||||||||||||||||
| 描述:对称正定矩阵 语法:
属性:
| ||||||||||||||||
| 描述:Moler 对称正定矩阵 语法:
属性:
| ||||||||||||||||
| 描述:源自离散纽曼问题的奇异矩阵(稀疏矩阵) 语法:
| ||||||||||||||||
| 描述:从标准正态(高斯)分布中随机采样的数值组成的数组 语法:
| ||||||||||||||||
| 描述:正交矩阵和准正交矩阵 语法:
| ||||||||||||||||
| 描述:Parter 矩阵 语法:
属性:
| ||||||||||||||||
| 描述:Pei 矩阵 语法:
| ||||||||||||||||
| 描述:来自 Poisson 方程的块三对角矩阵(稀疏矩阵) 语法:
| ||||||||||||||||
| 描述:Prolate 矩阵 语法:
属性:
| ||||||||||||||||
| 描述:具有归一化列和指定的奇异值的随机矩阵 语法:
| ||||||||||||||||
| 描述:具有指定特征值的随机相关矩阵 语法:
另请参阅: | ||||||||||||||||
| 描述:随机正交上黑森贝格矩阵 语法:
| ||||||||||||||||
| 描述:随机 J 正交矩阵 语法:
| ||||||||||||||||
| 描述:由元素 –1、0 或 1 组成的随机矩阵 语法:
| ||||||||||||||||
| 描述:具有预分配奇异值的随机矩阵 语法:
| ||||||||||||||||
| 描述:由 1 和 0 组成的 Redheffer 矩阵 语法:
属性:
| ||||||||||||||||
| 描述:与黎曼假设关联的矩阵 语法:
属性:
| ||||||||||||||||
| 描述:Ris 矩阵 语法:
| ||||||||||||||||
| 描述:具有病态整数特征值的非对称矩阵 语法:
属性:
| ||||||||||||||||
| 描述:具有“烟环”伪谱的复矩阵 语法:
属性:
| ||||||||||||||||
| 描述:对称正定托普利茨矩阵 语法:
| ||||||||||||||||
| 描述:五对角托普利茨矩阵(稀疏矩阵) 语法:
| ||||||||||||||||
| 描述:三对角矩阵(稀疏矩阵) 语法:
| ||||||||||||||||
| 描述:威尔金森和其他人讨论的上三角矩阵 语法:
属性:
| ||||||||||||||||
| 描述:标准均匀分布的随机采样数组成的数组 语法:
| ||||||||||||||||
| 描述:Wathen 矩阵(稀疏矩阵) 语法:
| ||||||||||||||||
| 描述:威尔金森设计或讨论的各种矩阵 语法:
|
输入参数,指定为标量、向量或矩阵。调用语法中使用的参数 P1,P2,...,Pn 取决于矩阵系列,如 matrixname 中的表中所述。
生成的测试矩阵的数据类型,指定为字符向量或字符串标量。
如果未指定
typename,则输出矩阵的数据类型由P1,P2,...,Pn中未指定矩阵维数或未选择选项来确定输出矩阵的字符的那些参量确定。如果这些参量中有任一参量的数据类型为single,则输出数据类型为single。否则,输出数据类型为double。对于所有测试矩阵,
typename必须为"double"或"single",除非matrixname是"integerdata"。如果matrixname是"integerdata",则typename可以是"double"、"single"、"int8"、"int16"、"int32"、"uint8"、"uint16"或"uint32"。
输出参量
输出系数、向量、矩阵或多维数组。调用语法所生成的输出 A1,A2,...,Am 取决于矩阵系列,如 matrixname 中的表中所述。在大多数情况下,gallery 函数只返回一个矩阵作为输出参量。
输出矩阵或多维数组。
参考
[1] The MATLAB® gallery of test matrices is based upon the work of Nicholas J. Higham at the Department of Mathematics, University of Manchester, Manchester, England. Further background can be found in the books MATLAB Guide, 2nd ed, by Desmond J. Higham and Nicholas J. Higham, Philadelphia: SIAM, 2005, and Accuracy and Stability of Numerical Algorithms, by Nicholas J. Higham, Philadelphia: SIAM, 1996.
[2] Graham, R.L. and N. J. A. Sloane. “Anti-Hadamard Matrices.“ Linear Algebra and Its Applications 62 (1984): 113-137.
[3] Lippold, G. “Todd, J., Basic Numerical Mathematics. Vol. 2: Numerical Algebra. ISNM 22. Basel-Stuttgart, Birkhäuser-Verlag 1977. 216 S. DM 48,–.“ ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 59, no. 10 (1979): 589–589.
[4] Gear, C. W. “A Simple Set of Test Matrices for Eigenvalue Programs.“ Mathematics of Computation 23, no. 105 (1969): 119-125.
[5] Lotkin, M. “A Set of Test Matrices.“ Mathematical Tables and Other Aids to Computation 9, no. 52 (1955): 153.
[6] Davies, P. I. and N. J. Higham. “Numerically Stable Generation of Correlation Matrices and Their Factors.” BIT Numerical Mathematics 40 (2000): 640-651.
[7] Barrett, W. W. and T. J. Jarvis. “Spectral Properties of a Matrix of Redheffer.“ Linear Algebra and Its Applications 162-164 (1992): 673-83.
[8] Roesler, F. “Riemann's Hypothesis as an Eigenvalue Problem.“ Linear Algebra and Its Applications 81 (1986): 153-98.
[9] Bondesson, L. and I. Traat. “A Nonsymmetric Matrix with Integer Eigenvalues.“ Linear and Multilinear Algebra 55, no. 3 (2007): 239-47.
[10] Rutishauser, H. “On Test Matrices.“ Programmation en Mathematiques Numeriques, Editions Centre Nat Recherche Sci, Paris, 165 (1966): 349-65.
[11] Wilkinson, J. H. The Algebraic Eigenvalue Problem. Monographs on Numerical Analysis. Oxford: Oxford; New York: Clarendon Press; Oxford University Press, 1988.
[12] Moler, C. B. Numerical Computing with MATLAB. Philadelphia: Society for Industrial and Applied Mathematics, 2004.
扩展功能
此函数完全支持基于线程的环境。有关详细信息,请参阅在基于线程的环境中运行 MATLAB 函数。
版本历史记录
在 R2006a 之前推出
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)