IIR 滤波器设计
此示例比较经典的巴特沃斯、切比雪夫和椭圆设计;并探索贝塞尔、尤尔-沃克和广义巴特沃斯滤波器。
IIR 与 FIR 滤波器的比较
与 FIR 滤波器相比,IIR 滤波器的主要优点是,要满足同一组设定,它的滤波器阶数通常远远低于 FIR 滤波器。虽然 IIR 滤波器具有非线性相位,但 MATLAB® 软件中的数据处理通常是“离线”执行的,即整个数据序列在滤波之前是可用的。这允许采用非因果零相位滤波方法(通过 filtfilt 函数),消除 IIR 滤波器的非线性相位失真。
经典 IIR 滤波器
经典的 IIR 滤波器、巴特沃斯滤波器、切比雪夫 I 型和 II 型滤波器滤波器、椭圆滤波器和贝塞尔滤波器都以不同的方式逼近理想的矩形滤波器。
Signal Processing Toolbox™ 提供的函数可在模拟域和数字域以及低通、高通、带通和带阻配置中创建所有上述类型的经典 IIR 滤波器(贝塞尔滤波器除外,因为它仅支持模拟情况)。对于大多数滤波器类型,您还可以在通带和阻带衰减以及过渡宽度方面找到符合给定滤波器设定的最低滤波器阶数。
其他 IIR 滤波器
直接滤波器设计函数 yulewalk 用于设计幅值响应接近指定频率响应函数的滤波器。这是创建多频带带通滤波器的一种方法。
您也可以使用参数化建模或系统辨识函数来设计 IIR 滤波器。这些函数在 Parametric Modeling 中有讨论。
广义巴特沃斯设计函数 maxflat 在广义巴特沃斯滤波器设计一节中有讨论。
IIR 滤波器方法概述
下表总结了使用 Signal Processing Toolbox™ 的各种滤波器方法,并列出可用于实现这些方法的函数。
工具箱滤波器方法和可用函数
滤波器方法 | 描述 | 滤波器函数 |
|---|---|---|
模拟原型 | 利用经典低通原型滤波器在连续(拉普拉斯)域中的零极点,通过频率变换和滤波器离散化获得数字滤波器。 | 滤波器设计:
阶估计函数: |
直接设计 | 通过逼近分段线性幅值响应,直接在离散时域中设计数字滤波器。 | |
广义巴特沃斯设计 | 设计零点多于极点的低通巴特沃斯滤波器。 | |
参数化建模 | 设计逼近规定的时域或频域响应的数字滤波器。(请参阅 System Identification Toolbox™ 文档,了解大量参数化建模工具。) | 时域建模: |
使用模拟原型的经典 IIR 滤波器设计
该工具箱提供的主要 IIR 数字滤波器设计方法基于将经典低通模拟滤波器转换为其等效的数字滤波器。以下各节说明如何设计滤波器,并总结了支持的滤波器类型的特征。有关滤波器设计过程的详细步骤,请参阅Special Topics in IIR Filter Design。
完成经典 IIR 滤波器设计
使用滤波器设计函数,您可以轻松创建具有低通、高通、带通或带阻 ftype 配置的任意阶滤波器。
滤波器设计函数
滤波器类型 | 设计函数 |
|---|---|
贝塞尔( |
|
巴特沃斯 ( |
|
切比雪夫 I 型 ( |
|
切比雪夫 II 型 ( |
|
椭圆 ( |
|
默认情况下,这些函数都返回低通滤波器;您只需指定所需的截止频率 Wn,以归一化单位表示(使奈奎斯特频率为 1 Hz)。要获得高通滤波器,请将 "high" 附加到函数的参数列表中。要获得带通或带阻滤波器,请将 Wn 指定为包含通带边缘频率的二元素向量。为带阻配置追加 "stop"。
以下是一些数字滤波器示例:
[bB,aB] = butter(5,0.4); % Lowpass Butterworth [bC1,aC1] = cheby1(4,1,[0.4 0.7]); % Bandpass Chebyshev Type I [bC2,aC2] = cheby2(6,60,0.8,"high"); % Highpass Chebyshev Type II [bE,aE] = ellip(3,1,60,[0.4 0.7],"stop"); % Bandstop elliptic
要设计一个模拟滤波器(可能是出于仿真需要),请在尾部添加参数 "s",以弧度/秒为单位指定截止频率:
[bBA,aBA] = butter(5,0.4,"s"); % Analog Butterworth filter
所有滤波器设计函数都会返回一个以传递函数、零极点增益或状态空间线性系统模型形式表示的滤波器,具体形式取决于存在多少输出参量。一般情况下,您应该避免使用传递函数形式,因为可能会发生舍入误差导致的数值问题。更好的做法是使用零极点增益形式,您可以使用 zp2sos 将其转换为二阶节 (SOS) 形式,然后使用 SOS 形式来分析或实现您的滤波器。
所有经典的 IIR 低通滤波器都不适用于极低的截止频率。因此,与其设计通带非常窄的低通 IIR 滤波器,不如设计更宽的通带并抽取输入信号。
按照频域设定设计 IIR 滤波器
Signal Processing Toolbox™ 提供阶选择函数,用于计算满足一组给定要求的最小滤波器阶。
滤波器类型 | 阶估计函数 |
|---|---|
巴特沃斯 |
|
切比雪夫 I 型 |
|
切比雪夫 II 型 |
|
椭圆 |
|
这些阶估计函数与滤波器设计函数结点合使用非常有用。假设您需要一个具有以下设定的带通滤波器:通带为 1000 至 2000 Hz,阻带从通带两侧外 500 Hz 处开始,采样频率为 10 kHz,通带波纹至多 1 dB,阻带衰减至少 60 dB。您可以通过使用以下 butter 函数来满足这些设定。
[n,Wn] = buttord([1000 2000]/5000,[500 2500]/5000,1,60)
n = 12
Wn = 1×2
0.1951 0.4080
[bB2,aB2] = butter(n,Wn);
满足相同要求的椭圆滤波器由下式给出
[n,Wn] = ellipord([1000 2000]/5000,[500 2500]/5000,1,60)
n = 5
Wn = 1×2
0.2000 0.4000
[bE2,aE2] = ellip(n,1,60,Wn);
这些函数也适用于其他标准频带配置以及模拟滤波器。
经典 IIR 滤波器类型的比较
Signal Processing Toolbox™ 提供五种不同类型的经典 IIR 滤波器,它们各有所长。本部分显示每种滤波器的基本模拟原型形式,并总结了主要特征。
巴特沃斯滤波器
巴特沃斯滤波器提供理想低通滤波器在模拟频率 和 处的响应的最佳泰勒级数逼近;对于任意阶 ,幅值平方响应在这两个位置的 阶导数为零(即在 和 处达到最大平坦)。总体而言,响应呈单调形态,从 到 平稳下降。在 处,。
n = 5; [z,p,k] = buttap(n); [bBp,aBp] = zp2tf(z,p,k); [hBp,wBp] = freqs(bBp,aBp,4096); semilogx(wBp,abs(hBp)) grid on xlabel("Frequency (rad/s)") ylabel("Magnitude")
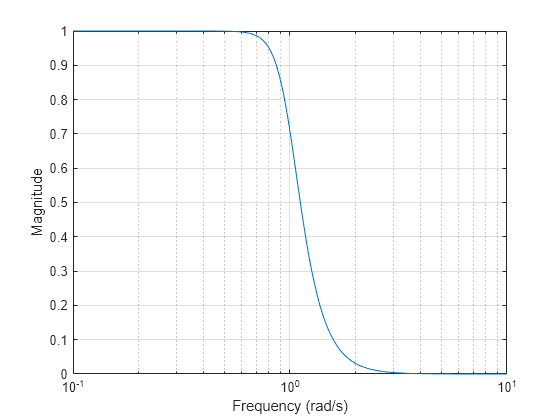
切比雪夫 I 型滤波器
切比雪夫 I 型滤波器通过在通带中引入 Rp dB 的等波纹,将整个通带的理想和实际频率响应之间的绝对差降至最低。其阻带响应达到最大平坦度。从通带到阻带的过渡比巴特沃斯滤波器更快。在 处,。
n = 5; Rp = 0.5; [z,p,k] = cheb1ap(n,Rp); [bC1p,aC1p] = zp2tf(z,p,k); [hC1p,wC1p] = freqs(bC1p,aC1p,4096); semilogx(wC1p,abs(hC1p)) grid on xlabel("Frequency (rad/s)") ylabel("Magnitude")
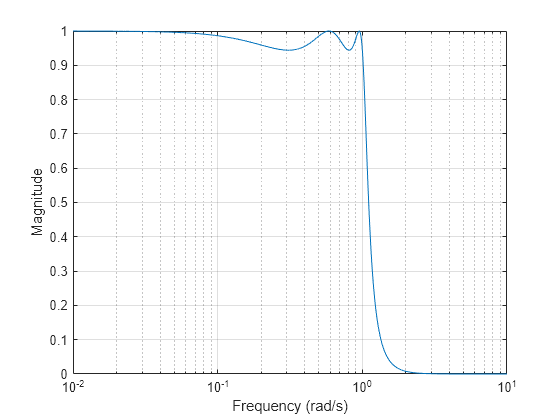
切比雪夫 II 型滤波器
切比雪夫 II 型滤波器通过在阻带中加入 Rs dB 的等波纹,将整个阻带的理想频率响应和实际频率响应之间的绝对差降至最低。其通带响应达到最大平坦度。
阻带不像 I 类滤波器那样快地逼近零(对于偶数滤波器阶 n 则根本不会逼近零)。然而,通带中没有波纹通常是重要优势。在 处,。
n = 5; Rs = 20; [z,p,k] = cheb2ap(n,Rs); [bC2p,aC2p] = zp2tf(z,p,k); [hC2p,wC2p] = freqs(bC2p,aC2p,4096); semilogx(wC2p,abs(hC2p)) grid on xlabel("Frequency (rad/s)") ylabel("Magnitude")
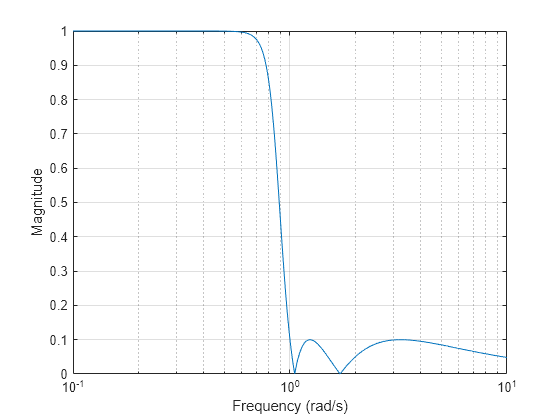
椭圆滤波器
椭圆滤波器在通带和阻带中均采用等波纹。它们通常以任何支持的滤波器类型中的最低阶满足滤波器要求。在给定滤波器阶数 n、以分贝为单位的通带波纹 Rp、以分贝为单位的阻带波纹 Rs 的情况下,椭圆滤波器可以最小化过渡宽度。在 处,。
n = 5; Rp = 0.5; Rs = 20; [z,p,k] = ellipap(n,Rp,Rs); [bEp,aEp] = zp2tf(z,p,k); [hEp,wEp] = freqs(bEp,aEp,4096); semilogx(wEp,abs(hEp)) grid on xlabel("Frequency (rad/s)") ylabel("Magnitude")
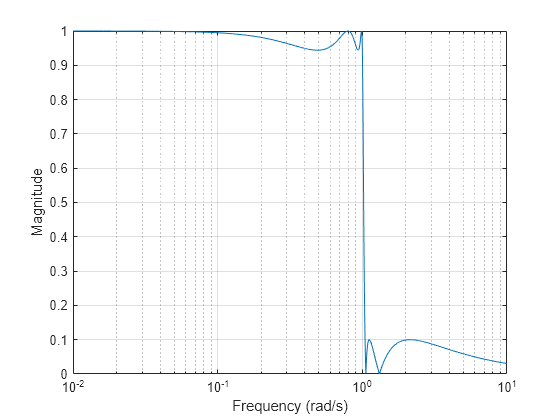
贝塞尔滤波器
模拟贝塞尔低通滤波器在零频率处具有最大平坦度的群延迟,并且在整个通带内保持几乎恒定的群延迟。因此,滤波后的信号在通带频率范围内保持其波形。当模拟贝塞尔低通滤波器通过频率映射转换为数字滤波器时,它不再具有这种最大平坦属性。Signal Processing Toolbox™ 仅支持使用完整贝塞尔滤波器设计函数实现模拟滤波器。
相比其他滤波器,贝塞尔滤波器通常需要更高的阶数才能获得理想的阻带衰减。在 处 ,并且会随着滤波器阶数 的增大而减小。
n = 5; [z,p,k] = besselap(n); [bBsp,aBsp] = zp2tf(z,p,k); [hBsp,wBsp] = freqs(bBsp,aBsp,4096); semilogx(wBsp,abs(hBsp)) grid on xlabel("Frequency (rad/s)") ylabel("Magnitude")
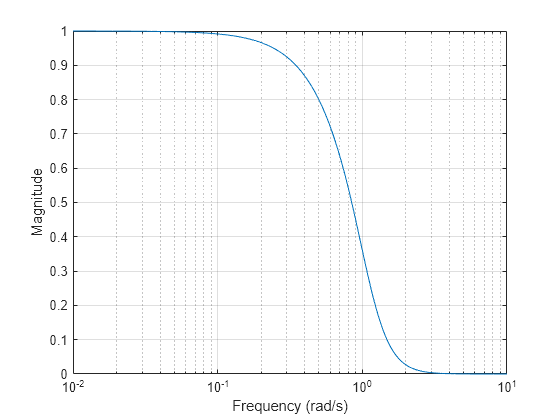
注意:上面显示的低通滤波器是用模拟原型函数 besselap、buttap、cheb1ap、cheb2ap 和 ellipap 创建的。这些函数求截止频率为 1 弧度/秒的适当类型的 n 阶模拟滤波器的零点、极点和增益。滤波器整体设计函数(besself、butter、cheby1、cheby2 和 ellip)将调用原型函数作为设计过程的第一步。有关详细信息,请参阅 Special Topics in IIR Filter Design。
直接 IIR 滤波器设计
此工具箱使用直接方法一词来说明 IIR 设计的方法,这些方法基于离散域中的设定设计滤波器。与模拟原型方法不同,直接设计方法不受标准低通、高通、带通或带阻配置的约束。相反,这些函数设计的滤波器具有任意(也许是多频带)频率响应。本部分讨论专门用于滤波器设计的 yulewalk 函数;Parametric Modeling讨论其他也比较直接的方法,如 Prony 方法、线性预测、Steiglitz-McBride 方法和逆频率设计。
yulewalk 函数通过拟合指定的频率响应来设计递归 IIR 数字滤波器。yulewalk 的名称反映其求滤波器分母系数的方法:它求理想的指定幅值平方响应的逆 FFT,并使用所得的自相关函数样本求解修正的尤尔-沃克方程。语句 [b,a] = yulewalk(n,f,m) 返回行向量 b 和 a,分别包含 n 阶 IIR 滤波器的 n+1 个分子系数和分母系数,该滤波器的频率幅值特征逼近向量 f 和 m 中给出的频率幅值特征。f 是频率点向量,范围从 0 到 1,其中 1 代表奈奎斯特频率。m 是向量,包含 f 中各点的指定幅值响应。f 和 m 可以说明任何分段线性形状幅值响应,包括多频带响应。此函数的对应 FIR 函数是 fir2,它还基于任意分段线性幅值响应设计滤波器。有关详细信息,请参阅 FIR 滤波器设计。
请注意,yulewalk 不接受相位信息,也不对最终滤波器的最佳性做出声明。
使用 yulewalk 设计多频带滤波器,并绘制指定和实际频率响应:
m = [0 0 1 1 0 0 1 1 0 0]; f = [0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 1]; [bY,aY] = yulewalk(10,f,m); freqz(bY,aY,128)
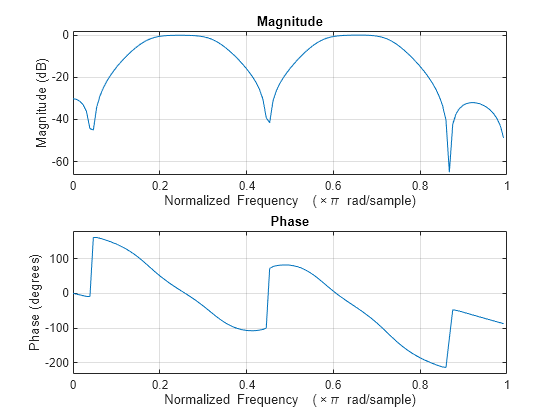
广义巴特沃斯滤波器设计
您可以使用函数 maxflat 设计广义巴特沃斯滤波器,即零极点数量不同的巴特沃斯滤波器。这非常适合一些极点比零点计算成本更高的实现。maxflat 与 butter 函数非常相似,区别在于使用前者时,您可以指定两个阶(分子阶与分母阶各一)而不是只指定一个。这些滤波器具有最大平坦度。这表示所得滤波器对于任何分子和分母阶均为最佳,即在 0 处和奈奎斯特频率 ω = π 处的最高阶导数均设置为 0。
例如,当两个阶相同时,maxflat 与 butter 相同:
[bM0,aM0] = maxflat(3,3,0.25)
bM0 = 1×4
0.0317 0.0951 0.0951 0.0317
aM0 = 1×4
1.0000 -1.4590 0.9104 -0.1978
[bB0,aB0] = butter(3,0.25)
bB0 = 1×4
0.0317 0.0951 0.0951 0.0317
aB0 = 1×4
1.0000 -1.4590 0.9104 -0.1978
但是,maxflat 函数更通用,因为它允许您设计零点多于极点的滤波器:
[bM1,aM1] = maxflat(3,1,0.25)
bM1 = 1×4
0.0950 0.2849 0.2849 0.0950
aM1 = 1×2
1.0000 -0.2402
maxflat 的第三个输入是半功率频率,该频率介于 0 和 1 之间,幅值响应为 1/√2。
您还可以使用 "sym" 选项设计具有最大平坦度属性的线性相位滤波器:
bM2 = maxflat(4,"sym",0.3)bM2 = 1×5
0.0331 0.2500 0.4337 0.2500 0.0331
比较滤波器响应:
filterAnalyzer(bM0,aM0,bM1,aM1,bM2,1, ... FilterNames=["SameOrder" "DiffOrder" "Symmetric"])
