lstmProjectedLayer
Long short-term memory (LSTM) projected layer for recurrent neural network (RNN)
Since R2022b
Description
An LSTM projected layer is an RNN layer that learns long-term dependencies between time steps in time-series and sequence data using projected learnable weights.
To compress a deep learning network, you can use projected layers. A projected layer is a type of deep learning layer that enables compression by reducing the number of stored learnable parameters. The layer introduces learnable projector matrices Q, replaces multiplications of the form , where W is a learnable matrix, with the multiplication , and stores Q and instead of storing W. Projecting x into a lower dimensional space using Q typically requires less memory to store the learnable parameters and can have similarly strong prediction accuracy.
Reducing the number of learnable parameters by projecting an LSTM layer rather than reducing the number of hidden units of the LSTM layer maintains the output size of the layer and, in turn, the sizes of the downstream layers, which can result in better prediction accuracy.
Creation
Syntax
Description
layer = lstmProjectedLayer(numHiddenUnits,outputProjectorSize,inputProjectorSize)NumHiddenUnits, OutputProjectorSize, and InputProjectorSize properties.
layer = lstmProjectedLayer(___,PropertyName=Value)OutputMode, HasStateInputs, HasStateOutputs, Activations, State, Parameters and Initialization, Learning Rate and Regularization, and Name properties using one or more name-value arguments.
Tip
To compress a neural network using projection, use the compressNetworkUsingProjection function.
Properties
Projected LSTM
Number of hidden units (also known as the hidden size), specified as a positive integer.
The number of hidden units corresponds to the amount of information that the layer remembers between time steps (the hidden state). The hidden state can contain information from all the previous time steps, regardless of the sequence length. If the number of hidden units is too large, then the layer can overfit to the training data. The hidden state does not limit the number of time steps that the layer processes in an iteration.
The layer outputs data with NumHiddenUnits channels.
To set this property, use the numHiddenUnits argument when you
create the LSTMProjectedLayer object. After you create a
LSTMProjectedLayer object, this property is read-only.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Output projector size, specified as a positive integer.
The LSTM layer operation uses four matrix multiplications of the form , where R denotes the recurrent weights and ht denotes the hidden state (or, equivalently, the layer output) at time step t.
The LSTM projected layer operation instead uses multiplications of the from , where Qo is a
NumHiddenUnits-by-OutputProjectorSize matrix known
as the output projector. The layer uses the same projector
Qo for each of the four
multiplications.
To perform the four multiplications of the form , an LSTM layer stores four recurrent weights matrices
R, which necessitates storing 4*NumHiddenUnits^2
learnable parameters. By instead storing the
4*NumHiddenUnits-by-OutputProjectorSize matrix and Qo, an LSTM projected layer
can perform the multiplication and store only 5*NumHiddenUnits*OutputProjectorSize
learnable parameters.
To set this property, use the outputProjectorSize argument
when you create the LSTMProjectedLayer object. After you create a
LSTMProjectedLayer object, this property is read-only.
Tip
To ensure that requires fewer learnable parameters, set the
OutputProjectorSize property to a value less than
4*NumHiddenUnits/5.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Input projector size, specified as a positive integer.
The LSTM layer operation uses four matrix multiplications of the form , where W denotes the input weights and xt denotes the layer input at time step t.
The LSTM projected layer operation instead uses multiplications of the from , where Qi is an
InputSize-by-InputProjectorSize matrix known as
the input projector. The layer uses the same projector
Qi for each of the four
multiplications.
To perform the four multiplications of the form , an LSTM layer stores four weight matrices W, which
necessitates storing 4*NumHiddenUnits*InputSize learnable parameters. By
instead storing the
4*NumHiddenUnits-by-InputProjectorSize matrix and Qi, an LSTM projected layer
can perform the multiplication and store only
(4*NumHiddenUnits+InputSize)*InputProjectorSize learnable
parameters.
To set this property, use the inputProjectorSize argument
when you create the LSTMProjectedLayer object. After you create a
LSTMProjectedLayer object, this property is read-only.
Tip
To ensure that requires fewer learnable parameters, set the
InputProjectorSize property to a value less than
4*NumHiddenUnits*inputSize/(4*NumHiddenUnits+inputSize).
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Output mode, specified as one of these values:
"sequence"— Output the complete sequence."last"— Output the last time step of the sequence.
The LSTMProjectedLayer object stores this property as a character vector.
To set this property, use the corresponding name-value argument when you create the LSTMProjectedLayer object. After you create a LSTMProjectedLayer object, this property is read-only.
This property is read-only.
Flag for state inputs to the layer, specified as 0
(false) or 1 (true).
If the HasStateInputs property is 0
(false), then the layer has one input with the name
"in", which corresponds to the input data. In this case, the layer
uses the HiddenState and CellState properties for the layer operation.
If the HasStateInputs property is 1
(true), then the layer has three inputs with the names
"in", "hidden", and "cell",
which correspond to the input data, hidden state, and cell state, respectively. In this
case, the layer uses the values passed to these inputs for the layer operation. If HasStateInputs is 1
(true), then the HiddenState and
CellState properties must be empty.
This property is read-only.
Flag for state outputs from the layer, specified as
0 (false) or
1
(true).
If the HasStateOutputs property is 0
(false), then the layer has one output with the name
"out", which corresponds to the output data.
If the HasStateOutputs property is 1
(true), then the layer has three outputs with the names
"out", "hidden", and
"cell", which correspond to the output data, hidden
state, and cell state, respectively. In this case, the layer also outputs the state
values that it computes.
This property is read-only.
Input size, specified as a positive integer or "auto". If
InputSize is "auto", then the software
automatically assigns the input size at training time.
If InputSize is "auto", then the
LSTMProjectedLayer object stores this property as a character
vector.
Data Types: double | char | string
Activations
This property is read-only.
Activation function to update the cell and hidden state, specified as one of these values:
"tanh"— Use the hyperbolic tangent function (tanh)."softsign"— Use the softsign function ."relu"(since R2024a) — Use the rectified linear unit (ReLU) function .
The software uses this option as the function in the calculations to update the cell and hidden state.
For more information on how an LSTM layer uses activation functions, see Long Short-Term Memory Layer.
The LSTMProjectedLayer object stores this property as a character vector.
Activation function to apply to the gates, specified as one of these values:
"sigmoid"— Use the sigmoid function, ."hard-sigmoid"— Use the hard sigmoid function,
The software uses this option as the function in the calculations for the layer gates.
The LSTMProjectedLayer object stores this property as a character vector.
To set this property, use the corresponding name-value argument when you create the LSTMProjectedLayer object. After you create a LSTMProjectedLayer object, this property is read-only.
State
Cell state to use in the layer operation, specified as a NumHiddenUnits-by-1 numeric vector. This value corresponds to the initial cell state when data is passed to the layer.
After you set this property manually, calls to the resetState
function set the cell state to this value.
If HasStateInputs is 1
(true), then the CellState
property must be empty.
Data Types: single | double
Hidden state to use in the layer operation, specified as a
NumHiddenUnits-by-1 numeric vector. This value corresponds to the
initial hidden state when data is passed to the layer.
After you set this property manually, calls to the resetState
function set the hidden state to this value.
If HasStateInputs is 1
(true), then the HiddenState
property must be empty.
Data Types: single | double
Parameters and Initialization
Function to initialize the input weights, specified as one of these values:
"glorot"— Initialize the input weights with the Glorot initializer [1] (also known as the Xavier initializer). The Glorot initializer independently samples from a uniform distribution with a mean of zero and a variance of2/(InputProjectorSize + numOut), wherenumOut = 4*NumHiddenUnits."he"— Initialize the input weights with the He initializer [2]. The He initializer samples from a normal distribution with a mean of zero and a variance of2/InputProjectorSize."orthogonal"— Initialize the input weights with Q, the orthogonal matrix in the QR decomposition of Z = QR for a random matrix Z sampled from a unit normal distribution [3]."narrow-normal"— Initialize the input weights by independently sampling from a normal distribution with a mean of zero and a standard deviation of 0.01."zeros"— Initialize the input weights with zeros."ones"— Initialize the input weights with ones.Function handle — Initialize the input weights with a custom function. If you specify a function handle, then the function must be of the form
weights = func(sz), whereszis the size of the input weights.
The layer only initializes the input weights when the InputWeights property is empty.
The LSTMProjectedLayer object stores this property as a character vector or a
function handle.
Data Types: char | string | function_handle
Function to initialize the recurrent weights, specified as one of the following:
"orthogonal"— Initialize the recurrent weights with Q, the orthogonal matrix in the QR decomposition of Z = QR for a random matrix Z sampled from a unit normal distribution [3]."glorot"— Initialize the recurrent weights with the Glorot initializer [1] (also known as the Xavier initializer). The Glorot initializer independently samples from a uniform distribution with a mean of zero and a variance of2/(numIn + numOut), wherenumIn = OutputProjectorSizeandnumOut = 4*NumHiddenUnits."he"— Initialize the recurrent weights with the He initializer [2]. The He initializer samples from a normal distribution with a mean of zero and a variance of2/OutputProjectorSize."narrow-normal"— Initialize the recurrent weights by independently sampling from a normal distribution with a mean of zero and a standard deviation of 0.01."zeros"— Initialize the recurrent weights with zeros."ones"— Initialize the recurrent weights with ones.Function handle — Initialize the recurrent weights with a custom function. If you specify a function handle, then the function must be of the form
weights = func(sz), whereszis the size of the recurrent weights.
The layer only initializes the recurrent weights when the RecurrentWeights property is empty.
The LSTMProjectedLayer object stores this property as a character vector or a
function handle.
Data Types: char | string | function_handle
Function to initialize the input projector, specified as one of these values:
"orthogonal"— Initialize the input projector with Q, the orthogonal matrix in the QR decomposition of Z = QR for a random matrix Z sampled from a unit normal distribution [3]."glorot"— Initialize the input projector with the Glorot initializer [1] (also known as the Xavier initializer). The Glorot initializer independently samples from a uniform distribution with a mean of zero and a variance of2/(InputSize + inputProjectorSize)."he"— Initialize the input projector with the He initializer [2]. The He initializer samples from a normal distribution with a mean of zero and a variance of2/InputSize."narrow-normal"— Initialize the input projector by independently sampling from a normal distribution with a mean of zero and a standard deviation of 0.01."zeros"— Initialize the input projector with zeros."ones"— Initialize the input projector with ones.Function handle — Initialize the input projector with a custom function. If you specify a function handle, then the function must have the form
weights = func(sz), whereszis the size of the input projector.
The layer initializes the input projector only when the InputProjector property is empty.
The LSTMProjectedLayer object stores this property as a character vector or a
function handle.
Data Types: char | string | function_handle
Function to initialize the output projector, specified as one of these values:
"orthogonal"— Initialize the output projector with Q, the orthogonal matrix in the QR decomposition of Z = QR for a random matrix Z sampled from a unit normal distribution [3]."glorot"— Initialize the output projector with the Glorot initializer [1] (also known as the Xavier initializer). The Glorot initializer independently samples from a uniform distribution with a mean of zero and a variance of2/(NumHiddenUnits + OutputProjectorSize)."he"— Initialize the output projector with the He initializer [2]. The He initializer samples from a normal distribution with a mean of zero and a variance of2/NumHiddenUnits."narrow-normal"— Initialize the output projector by independently sampling from a normal distribution with a mean of zero and a standard deviation of 0.01."zeros"— Initialize the output projector with zeros."ones"— Initialize the output projector with ones.Function handle — Initialize the output projector with a custom function. If you specify a function handle, then the function must have the form
weights = func(sz), whereszis the size of the output projector.
The layer initializes the output projector only when the OutputProjector property is empty.
The LSTMProjectedLayer object stores this property as a character vector or a
function handle.
Data Types: char | string | function_handle
Function to initialize the bias, specified as one of these values:
"unit-forget-gate"— Initialize the forget gate bias with ones and the remaining biases with zeros."narrow-normal"— Initialize the bias by independently sampling from a normal distribution with zero mean and a standard deviation of 0.01."ones"— Initialize the bias with ones.Function handle — Initialize the bias with a custom function. If you specify a function handle, then the function must be of the form
bias = func(sz), whereszis the size of the bias.
The layer only initializes the bias when the Bias property is
empty.
The LSTMProjectedLayer object stores this property as a character vector or a
function handle.
Data Types: char | string | function_handle
Input weights, specified as a matrix.
The input weight matrix is a concatenation of the four input weight matrices for the components (gates) in the layer operation. The layer vertically concatenates the four matrices in this order:
Input gate
Forget gate
Cell candidate
Output gate
The input weights are learnable parameters. When you train a
neural network using the trainnet function,
if InputWeights is nonempty, then the software uses the
InputWeights property as the initial value. If InputWeights is empty, then the software uses the initializer
specified by InputWeightsInitializer.
At training time, InputWeights is a
4*NumHiddenUnits-by-InputProjectorSize
matrix.
Recurrent weights, specified as a matrix.
The recurrent weight matrix is a concatenation of the four recurrent weight matrices for the components (gates) in the layer operation. The layer vertically concatenates the four matrices in this order:
Input gate
Forget gate
Cell candidate
Output gate
The recurrent weights are learnable parameters. When you train
an RNN using the trainnet function,
if RecurrentWeights is nonempty, then the software uses the
RecurrentWeights property as the initial value. If
RecurrentWeights is empty, then the software uses the
initializer specified by RecurrentWeightsInitializer.
At training time, RecurrentWeights is a
4*NumHiddenUnits-by-OutputProjectorSize
matrix.
Input projector, specified as a matrix.
The input projector weights are learnable parameters. When you train a network using the
trainnet
function, if InputProjector is nonempty, then the
software uses the InputProjector property as the
initial value. If InputProjector is empty, then the
software uses the initializer specified by InputProjectorInitializer.
At training time, InputProjector is a InputSize-by-InputProjectorSize matrix.
Data Types: single | double
Output projector, specified as a matrix.
The output projector weights are learnable parameters. When you train a network using the
trainnet
function, if OutputProjector is nonempty, then the
software uses the OutputProjector property as the
initial value. If OutputProjector is empty, then the
software uses the initializer specified by OutputProjectorInitializer.
At training time, OutputProjector is a NumHiddenUnits-by-OutputProjectorSize matrix.
Data Types: single | double
Layer biases, specified as a numeric vector.
The bias vector is a concatenation of the four bias vectors for the components (gates) in the layer. The layer vertically concatenates the four vectors in this order:
Input gate
Forget gate
Cell candidate
Output gate
The layer biases are learnable parameters. When you train a neural network, if Bias is nonempty, then the trainnet
function uses the Bias property as the initial value. If
Bias is empty, then software uses the initializer
specified by BiasInitializer.
At training time, Bias is a
4*NumHiddenUnits-by-1 numeric vector.
Learning Rate and Regularization
Learning rate factor for the input weights, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global learning rate
to determine the learning rate factor for the input weights of the layer. For example, if
InputWeightsLearnRateFactor is 2, then the learning
rate factor for the input weights of the layer is twice the current global learning rate. The
software determines the global learning rate based on the settings you specify with the
trainingOptions function.
To control the value of the learning rate factor for the four individual matrices in
InputWeights, specify a 1-by-4 vector. The
entries of InputWeightsLearnRateFactor correspond to
the learning rate factor of these components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the matrices, specify a nonnegative scalar.
Example: 2
Example: [1 2 1 1]
Learning rate factor for the recurrent weights, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global learning rate
to determine the learning rate for the recurrent weights of the layer. For example, if
RecurrentWeightsLearnRateFactor is 2, then the
learning rate for the recurrent weights of the layer is twice the current global learning rate.
The software determines the global learning rate based on the settings you specify using the
trainingOptions function.
To control the value of the learning rate factor for the four individual matrices in
RecurrentWeights, specify a 1-by-4 vector. The
entries of RecurrentWeightsLearnRateFactor correspond
to the learning rate factor of these components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the matrices, specify a nonnegative scalar.
Example: 2
Example: [1 2 1 1]
Learning rate factor for the input projector, specified as a nonnegative scalar.
The software multiplies this factor by the global learning rate to determine the learning rate factor for the input projector of the layer. For example, if InputProjectorLearnRateFactor is 2, then the learning rate factor for the input projector of the layer is twice the current global learning rate. The software determines the global learning rate based on the settings you specify using the trainingOptions function.
Learning rate factor for the output projector, specified as a nonnegative scalar.
The software multiplies this factor by the global learning rate to determine the learning rate factor for the output projector of the layer. For example, if OutputProjectorLearnRateFactor is 2, then the learning rate factor for the output projector of the layer is twice the current global learning rate. The software determines the global learning rate based on the settings you specify using the trainingOptions function.
Learning rate factor for the biases, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global learning rate to determine the learning rate for the biases in this layer. For example, if BiasLearnRateFactor is 2, then the learning rate for the biases in the layer is twice the current global learning rate. The software determines the global learning rate based on the settings you specify using the trainingOptions function.
To control the value of the learning rate factor for the four individual vectors in
Bias, specify a 1-by-4 vector. The entries of
BiasLearnRateFactor correspond to the learning rate factor of
these components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the vectors, specify a nonnegative scalar.
Example:
2
Example:
[1 2 1 1]
L2 regularization factor for the input weights, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global
L2 regularization factor to determine the
L2 regularization factor for the input weights
of the layer. For example, if InputWeightsL2Factor is 2,
then the L2 regularization factor for the input
weights of the layer is twice the current global L2
regularization factor. The software determines the L2
regularization factor based on the settings you specify using the trainingOptions function.
To control the value of the L2
regularization factor for the four individual matrices in
InputWeights, specify a 1-by-4 vector. The
entries of InputWeightsL2Factor correspond to the
L2 regularization
factor of these components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the matrices, specify a nonnegative scalar.
Example: 2
Example:
[1 2 1 1]
L2 regularization factor for the recurrent weights, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global
L2 regularization factor to determine the
L2 regularization factor for the recurrent
weights of the layer. For example, if RecurrentWeightsL2Factor is
2, then the L2 regularization
factor for the recurrent weights of the layer is twice the current global
L2 regularization factor. The software
determines the L2 regularization factor based on the
settings you specify using the trainingOptions function.
To control the value of the L2
regularization factor for the four individual matrices in
RecurrentWeights, specify a 1-by-4 vector. The
entries of RecurrentWeightsL2Factor correspond to the
L2 regularization
factor of these components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the matrices, specify a nonnegative scalar.
Example: 2
Example:
[1 2 1 1]
L2 regularization factor for the input projector, specified as a nonnegative scalar.
The software multiplies this factor by the global L2 regularization factor to determine the L2 regularization factor for the input projector of the layer. For example, if InputProjectorL2Factor is 2, then the L2 regularization factor for the input projector of the layer is twice the current global L2 regularization factor. The software determines the global L2 regularization factor based on the settings you specify using the trainingOptions function.
L2 regularization factor for the output projector, specified as a nonnegative scalar.
The software multiplies this factor by the global L2 regularization factor to determine the L2 regularization factor for the output projector of the layer. For example, if OutputProjectorL2Factor is 2, then the L2 regularization factor for the output projector of the layer is twice the current global L2 regularization factor. The software determines the global L2 regularization factor based on the settings you specify using the trainingOptions function.
L2 regularization factor for the biases, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global L2 regularization factor to determine the L2 regularization for the biases in this layer. For example, if BiasL2Factor is 2, then the L2 regularization for the biases in this layer is twice the global L2 regularization factor. The software determines the global L2 regularization factor based on the settings you specify using the trainingOptions function.
To control the value of the L2
regularization factor for the four individual vectors in Bias,
specify a 1-by-4 vector. The entries of BiasL2Factor correspond to
the L2 regularization factor of these
components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the vectors, specify a nonnegative scalar.
Example:
2
Example:
[1 2 1 1]
Layer
This property is read-only.
Number of inputs to the layer.
If the HasStateInputs property is 0
(false), then the layer has one input with the name
"in", which corresponds to the input data. In this case, the layer
uses the HiddenState and CellState properties for the layer operation.
If the HasStateInputs property is 1
(true), then the layer has three inputs with the names
"in", "hidden", and "cell",
which correspond to the input data, hidden state, and cell state, respectively. In this
case, the layer uses the values passed to these inputs for the layer operation. If HasStateInputs is 1
(true), then the HiddenState and
CellState properties must be empty.
Data Types: double
This property is read-only.
Input names of the layer.
If the HasStateInputs property is 0
(false), then the layer has one input with the name
"in", which corresponds to the input data. In this case, the layer
uses the HiddenState and CellState properties for the layer operation.
If the HasStateInputs property is 1
(true), then the layer has three inputs with the names
"in", "hidden", and "cell",
which correspond to the input data, hidden state, and cell state, respectively. In this
case, the layer uses the values passed to these inputs for the layer operation. If HasStateInputs is 1
(true), then the HiddenState and
CellState properties must be empty.
The LSTMProjectedLayer object stores this property as a cell array of character
vectors.
This property is read-only.
Number of outputs to the layer.
If the HasStateOutputs property is 0
(false), then the layer has one output with the name
"out", which corresponds to the output data.
If the HasStateOutputs property is 1
(true), then the layer has three outputs with the names
"out", "hidden", and
"cell", which correspond to the output data, hidden
state, and cell state, respectively. In this case, the layer also outputs the state
values that it computes.
Data Types: double
This property is read-only.
Output names of the layer.
If the HasStateOutputs property is 0
(false), then the layer has one output with the name
"out", which corresponds to the output data.
If the HasStateOutputs property is 1
(true), then the layer has three outputs with the names
"out", "hidden", and
"cell", which correspond to the output data, hidden
state, and cell state, respectively. In this case, the layer also outputs the state
values that it computes.
The LSTMProjectedLayer object stores this property as a cell array of character
vectors.
Examples
Create an LSTM projected layer with 100 hidden units, an output projector size of 30, an input projector size of 16, and the name "lstmp".
layer = lstmProjectedLayer(100,30,16,Name="lstmp")layer =
LSTMProjectedLayer with properties:
Name: 'lstmp'
InputNames: {'in'}
OutputNames: {'out'}
NumInputs: 1
NumOutputs: 1
HasStateInputs: 0
HasStateOutputs: 0
Hyperparameters
InputSize: 'auto'
NumHiddenUnits: 100
InputProjectorSize: 16
OutputProjectorSize: 30
OutputMode: 'sequence'
StateActivationFunction: 'tanh'
GateActivationFunction: 'sigmoid'
Learnable Parameters
InputWeights: []
RecurrentWeights: []
Bias: []
InputProjector: []
OutputProjector: []
State Parameters
HiddenState: []
CellState: []
Show all properties
Include an LSTM projected layer in a layer array.
inputSize = 12;
numHiddenUnits = 100;
outputProjectorSize = max(1,floor(0.75*numHiddenUnits));
inputProjectorSize = max(1,floor(0.25*inputSize));
layers = [
sequenceInputLayer(inputSize)
lstmProjectedLayer(numHiddenUnits,outputProjectorSize,inputProjectorSize)
fullyConnectedLayer(10)
softmaxLayer];Compare the sizes of networks that do and do not contain projected layers.
Define an LSTM network architecture. Specify the input size as 12, which corresponds to the number of features of the input data. Configure an LSTM layer with 100 hidden units that outputs the last element of the sequence. Finally, specify nine classes by including a fully connected layer of size 9, followed by a softmax layer and a classification layer.
inputSize = 12; numHiddenUnits = 100; numClasses = 9; layers = [ ... sequenceInputLayer(inputSize) lstmLayer(numHiddenUnits,OutputMode="last") fullyConnectedLayer(numClasses) softmaxLayer classificationLayer]
layers =
5×1 Layer array with layers:
1 '' Sequence Input Sequence input with 12 dimensions
2 '' LSTM LSTM with 100 hidden units
3 '' Fully Connected 9 fully connected layer
4 '' Softmax softmax
5 '' Classification Output crossentropyex
Analyze the network using the analyzeNetwork function. The network has approximately 46,100 learnable parameters.
analyzeNetwork(layers)
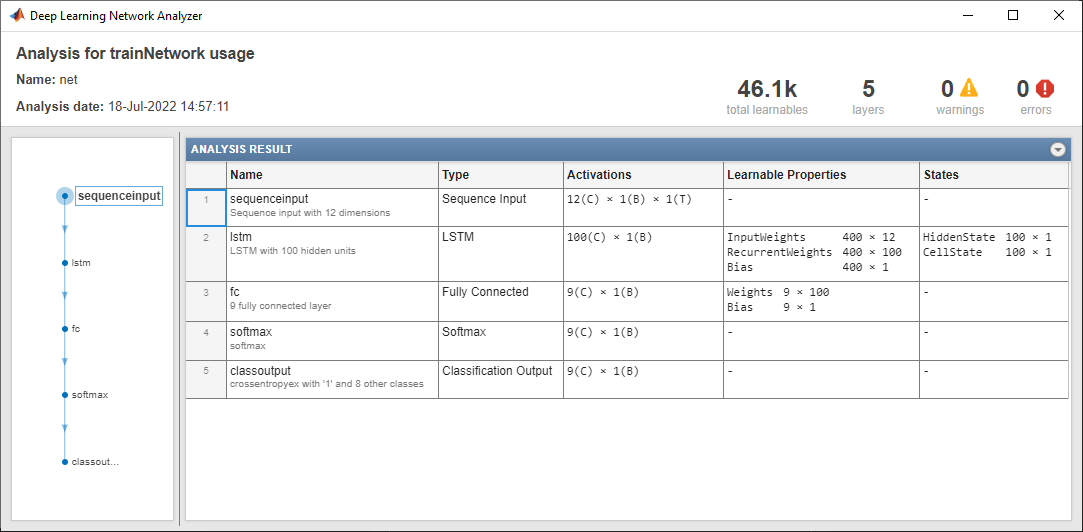
Create an identical network with an LSTM projected layer in place of the LSTM layer.
For the LSTM projected layer:
Specify the same number of hidden units as the LSTM layer
Specify an output projector size of 25% of the number of hidden units.
Specify an input projector size of 75% of the input size.
Ensure that the output and input projector sizes are positive by taking the maximum of the sizes and 1.
outputProjectorSize = max(1,floor(0.25*numHiddenUnits)); inputProjectorSize = max(1,floor(0.75*inputSize)); layersProjected = [ ... sequenceInputLayer(inputSize) lstmProjectedLayer(numHiddenUnits,outputProjectorSize,inputProjectorSize,OutputMode="last") fullyConnectedLayer(numClasses) softmaxLayer classificationLayer];
Analyze the network using the analyzeNetwork function. The network has approximately 17,500 learnable parameters, which is a reduction of more than half. The sizes of the learnable parameters of the layers following the projected layer have the same sizes as the network without the LSTM projected layer. Reducing the number of learnable parameters by projecting an LSTM layer rather than reducing the number of hidden units of the LSTM layer maintains the output size of the layer and, in turn, the sizes of the downstream layers, which can result in better prediction accuracy.
analyzeNetwork(layersProjected)

Algorithms
An LSTM layer is an RNN layer that learns long-term dependencies between time steps in time-series and sequence data.
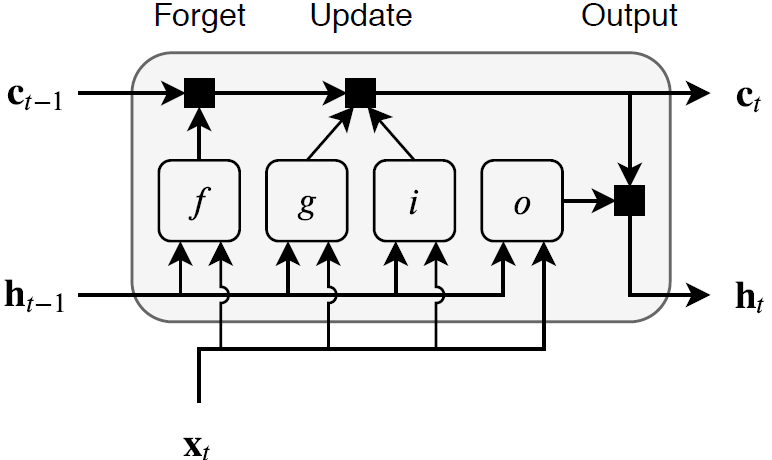
The state of the layer consists of the hidden state (also known as the output state) and the cell state. The hidden state at time step t contains the output of the LSTM layer for this time step. The cell state contains information learned from the previous time steps. At each time step, the layer adds information to or removes information from the cell state. The layer controls these updates using gates.
These components control the cell state and hidden state of the layer.
| Component | Purpose |
|---|---|
| Input gate (i) | Control level of cell state update |
| Forget gate (f) | Control level of cell state reset (forget) |
| Cell candidate (g) | Add information to cell state |
| Output gate (o) | Control level of cell state added to hidden state |
This diagram illustrates the flow of data at time step t. This diagram shows how the gates forget, update, and output the cell and hidden states.
The learnable weights of an LSTM layer are the input weights W
(InputWeights), the recurrent weights R
(RecurrentWeights), and the bias b
(Bias). The matrices W, R,
and b are concatenations of the input weights, the recurrent weights, and
the bias of each component, respectively. The layer concatenates the matrices according to
these equations:
where i, f, g, and o denote the input gate, forget gate, cell candidate, and output gate, respectively.
The cell state at time step t is given by
where denotes the Hadamard product (element-wise multiplication of vectors).
The hidden state at time step t is given by
where denotes the state activation function. By default, the
lstmLayer function uses the hyperbolic tangent function (tanh) to
compute the state activation function.
These formulas describe the components at time step t.
| Component | Formula |
|---|---|
| Input gate | |
| Forget gate | |
| Cell candidate | |
| Output gate |
In these calculations, denotes the gate activation function. By default, the
lstmLayer function, uses the sigmoid function, given by , to compute the gate activation function.
An LSTM projected layer is an RNN layer that learns long-term dependencies between time steps in time-series and sequence data using projected learnable weights.
To compress a deep learning network, you can use projected layers. A projected layer is a type of deep learning layer that enables compression by reducing the number of stored learnable parameters. The layer introduces learnable projector matrices Q, replaces multiplications of the form , where W is a learnable matrix, with the multiplication , and stores Q and instead of storing W. Projecting x into a lower dimensional space using Q typically requires less memory to store the learnable parameters and can have similarly strong prediction accuracy.
Reducing the number of learnable parameters by projecting an LSTM layer rather than reducing the number of hidden units of the LSTM layer maintains the output size of the layer and, in turn, the sizes of the downstream layers, which can result in better prediction accuracy.
The LSTM layer operation uses four matrix multiplications of the form , where R denotes the recurrent weights and ht denotes the hidden state (or, equivalently, the layer output) at time step t.
The LSTM projected layer operation instead uses multiplications of the from , where Qo is a
NumHiddenUnits-by-OutputProjectorSize matrix known
as the output projector. The layer uses the same projector
Qo for each of the four
multiplications.
To perform the four multiplications of the form , an LSTM layer stores four recurrent weights matrices
R, which necessitates storing 4*NumHiddenUnits^2
learnable parameters. By instead storing the
4*NumHiddenUnits-by-OutputProjectorSize matrix and Qo, an LSTM projected layer
can perform the multiplication and store only 5*NumHiddenUnits*OutputProjectorSize
learnable parameters.
The LSTM layer operation uses four matrix multiplications of the form , where W denotes the input weights and xt denotes the layer input at time step t.
The LSTM projected layer operation instead uses multiplications of the from , where Qi is an
InputSize-by-InputProjectorSize matrix known as
the input projector. The layer uses the same projector
Qi for each of the four
multiplications.
To perform the four multiplications of the form , an LSTM layer stores four weight matrices W, which
necessitates storing 4*NumHiddenUnits*InputSize learnable parameters. By
instead storing the
4*NumHiddenUnits-by-InputProjectorSize matrix and Qi, an LSTM projected layer
can perform the multiplication and store only
(4*NumHiddenUnits+InputSize)*InputProjectorSize learnable
parameters.
Layers in a layer array or layer graph pass data to subsequent layers as formatted dlarray objects.
The format of a dlarray object is a string of characters in which each
character describes the corresponding dimension of the data. The format consists of one or
more of these characters:
"S"— Spatial"C"— Channel"B"— Batch"T"— Time"U"— Unspecified
For example, you can describe 2-D image data that is represented as a 4-D array, where the
first two dimensions correspond to the spatial dimensions of the images, the third
dimension corresponds to the channels of the images, and the fourth dimension
corresponds to the batch dimension, as having the format "SSCB"
(spatial, spatial, channel, batch).
You can interact with these dlarray objects in automatic differentiation
workflows, such as those for developing a custom layer, using a functionLayer
object, or using the forward and predict functions with
dlnetwork objects.
This table shows the supported input formats of LSTMProjectedLayer objects and the
corresponding output format. If the software passes the output of the layer to a custom
layer that does not inherit from the nnet.layer.Formattable class, or a
FunctionLayer object with the Formattable property
set to 0 (false), then the layer receives an
unformatted dlarray object with dimensions ordered according to the formats
in this table. The formats listed here are only a subset. The layer may support additional
formats such as formats with additional "S" (spatial) or
"U" (unspecified) dimensions.
| Input Format | OutputMode | Output Format |
|---|---|---|
| "sequence" |
|
"last" | ||
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
In dlnetwork objects, LSTMProjectedLayer objects also support these input and output format combinations.
| Input Format | OutputMode | Output Format |
|---|---|---|
| "sequence" |
|
"last" | ||
| "sequence" | |
"last" | ||
| "sequence" | |
"last" | ||
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" | ||
| "sequence" | |
"last" | ||
| "sequence" | |
"last" | ||
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" | ||
| "sequence" | |
"last" | ||
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
|
If the HasStateInputs property is 1
(true), then the layer has two additional inputs with the names
"hidden" and "cell", which correspond to the
hidden state and cell state, respectively. These additional inputs expect input format
"CB" (channel, batch).
If the HasStateOutputs property is 1
(true), then the layer has two additional outputs with names
"hidden" and "cell", which correspond to the
hidden state and cell state, respectively. These additional outputs have output format
"CB" (channel, batch).
References
[1] Glorot, Xavier, and Yoshua Bengio. "Understanding the Difficulty of Training Deep Feedforward Neural Networks." In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 249–356. Sardinia, Italy: AISTATS, 2010. https://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf
[2] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. "Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification." In 2015 IEEE International Conference on Computer Vision (ICCV), 1026–34. Santiago, Chile: IEEE, 2015. https://doi.org/10.1109/ICCV.2015.123
[3] Saxe, Andrew M., James L. McClelland, and Surya Ganguli. "Exact Solutions to the Nonlinear Dynamics of Learning in Deep Linear Neural Networks.” Preprint, submitted February 19, 2014. https://arxiv.org/abs/1312.6120.
Extended Capabilities
Usage notes and limitations:
LSTM projected layer objects support generic C and C++ code generation only.
Code generation does not support passing
dlarrayobjects with unspecified (U) dimensions to this layer.For code generation, you must pass a
dlarrayobject with a channel (C) dimension as the input to this layer. For example, code generation supports data format such as "SSC" or "SSCBT".
Usage notes and limitations:
LSTM projected layer objects only support generating CUDA code generation that does not depend on third-party libraries.
Code generation does not support passing
dlarrayobjects with unspecified (U) dimensions to this layer.For code generation, you must pass a
dlarrayobject with a channel (C) dimension as the input to this layer. For example, code generation supports data format such as "SSC" or "SSCBT".
Version History
Introduced in R2022bYou can set the StateActivationFunction property to "relu", when
generating generic C/C++ or plain CUDA code that does not depend on any third-party
libraries.
To specify the ReLU state activation function, set the StateActivationFunction property to "relu".
See Also
compressNetworkUsingProjection | neuronPCA | trainingOptions | trainnet | ProjectedLayer | gruProjectedLayer | lstmLayer | exportNetworkToSimulink | LSTM Projected Layer
Topics
- Train Network with LSTM Projected Layer
- Compress Neural Network Using Projection
- Sequence Classification Using Deep Learning
- Sequence Classification Using 1-D Convolutions
- Time Series Forecasting Using Deep Learning
- Sequence-to-Sequence Classification Using Deep Learning
- Sequence-to-Sequence Regression Using Deep Learning
- Sequence-to-One Regression Using Deep Learning
- Classify Videos Using Deep Learning
- Long Short-Term Memory Neural Networks
- List of Deep Learning Layers
- Deep Learning Tips and Tricks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)