butter

Butterworth filter design

collapse all in page

Syntax

[b,a] = butter(n,Wn)

[b,a] = butter(n,Wn,ftype)

[z,p,k] = butter(___)

[A,B,C,D] = butter(___)

[___] = butter(___,"s")

[B,A] = butter(n,Wn,"ctf")

[___] = butter(n,Wn,ftype,"ctf")

[___,gS] = butter(___)

Description

[b,a] = butter(n,Wn) designs an nth-order lowpass digital Butterworth filter with normalized cutoff frequency Wn. The butter function returns the numerator and denominator coefficients of the filter transfer function.

example

[b,a] = butter(n,Wn,ftype) designs a lowpass, highpass, bandpass, or bandstop digital Butterworth filter, depending on the value of ftype and the number of elements of Wn. The resulting bandpass and bandstop filter designs are of order 2n.

Note

You might encounter numerical instabilities when designing IIR filters with transfer functions for orders as low as 4. See Transfer Functions and CTF for more information about numerical issues that affect forming the transfer function.

example

[z,p,k] = butter(___) designs a digital Butterworth filter and returns its zeros, poles, and gain. This syntax can include any of the input arguments in previous syntaxes.

example

[A,B,C,D] = butter(___) designs a digital Butterworth filter and returns the matrices that specify its state-space representation.

example

[___] = butter(___,"s") designs an analog Butterworth filter using any of the input or output arguments in previous syntaxes.

example

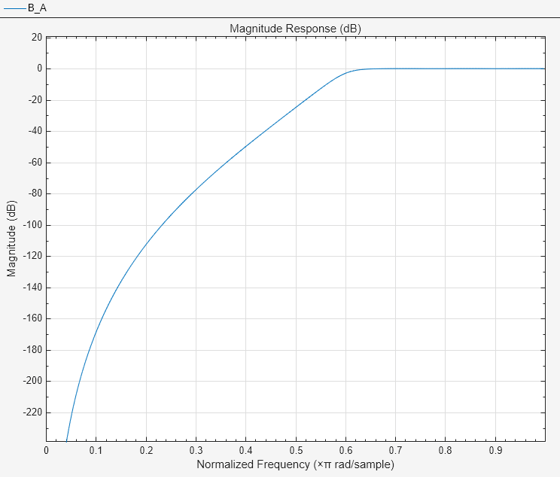
[B,A] = butter(n,Wn,"ctf") designs a lowpass digital Butterworth filter using second-order Cascaded Transfer Functions (CTF). The function returns matrices that list the denominator and numerator polynomial coefficients of the filter transfer function, represented as a cascade of filter sections. This approach generates IIR filters with improved numerical stability compared to with single-section transfer functions. (since R2024b)

[___] = butter(n,Wn,ftype,"ctf") designs a lowpass, highpass, bandpass, or bandstop digital Butterworth filter, and returns the filter representation using the CTF format. The resulting design sections are of order 2 (lowpass and highpass filters) or 4 (bandpass and bandstop filters). (since R2024b)

example

[___,gS] = butter(___) also returns the overall gain of the system. You must specify "ctf" to return gS. (since R2024b)

Examples

collapse all

Lowpass Butterworth Transfer Function

Open Live Script

Design a 6th-order lowpass Butterworth filter with a cutoff frequency of 300 Hz, which, for data sampled at 1000 Hz, corresponds to $0.6 π$ rad/sample. Plot its magnitude and phase responses. Use it to filter a 1000-sample random signal.

fc = 300;
fs = 1000;

[b,a] = butter(6,fc/(fs/2));

freqz(b,a,[],fs)

subplot(2,1,1)
ylim([-100 20])

Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Frequency (Hz), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Frequency (Hz), ylabel Magnitude (dB) contains an object of type line.

dataIn = randn(1000,1);
dataOut = filter(b,a,dataIn);

Bandstop Butterworth Filter

Open Live Script

Design a 6th-order Butterworth bandstop filter with normalized edge frequencies of $0.2 π$ and $0.6 π$ rad/sample. Plot its magnitude and phase responses. Use it to filter random data.

[b,a] = butter(3,[0.2 0.6],'stop');
freqz(b,a)

$Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.$

dataIn = randn(1000,1);
dataOut = filter(b,a,dataIn);

Highpass Butterworth Filter

Open Live Script

Design a 9th-order highpass Butterworth filter. Specify a cutoff frequency of 300 Hz, which, for data sampled at 1000 Hz, corresponds to $0.6 π$ rad/sample. Plot the magnitude and phase responses. Convert the zeros, poles, and gain to second-order sections. Display the frequency response of the filter.

[z,p,k] = butter(9,300/500,"high");
sos = zp2sos(z,p,k);
freqz(sos)

Bandpass Butterworth Filter

Open Live Script

Design a 20th-order Butterworth bandpass filter with a lower cutoff frequency of 500 Hz and a higher cutoff frequency of 560 Hz. Specify a sample rate of 1500 Hz. Use the state-space representation. Convert the state-space representation to second-order sections. Visualize the frequency responses.

fs = 1500;
[A,B,C,D] = butter(10,[500 560]/(fs/2));
sos = ss2sos(A,B,C,D);
freqz(sos,[],fs)

Design an identical filter using designfilt. Visualize the frequency responses.

d = designfilt("bandpassiir",FilterOrder=20, ...
    HalfPowerFrequency1=500,HalfPowerFrequency2=560, ...
    SampleRate=fs);
freqz(d,[],fs)

Comparison of Analog IIR Lowpass Filters

Open Live Script

Design a fifth-order analog Butterworth lowpass filter with a cutoff frequency of 2 GHz. Multiply by $2 π$ to convert the frequency to radians per second. Compute the frequency response of the filter at 4096 points.

n = 5;
wc = 2*pi*2e9;
w = 2*pi*1e9*logspace(-2,1,4096)';

[zb,pb,kb] = butter(n,wc,"s");
[bb,ab] = zp2tf(zb,pb,kb);
[hb,wb] = freqs(bb,ab,w);
gdb = -diff(unwrap(angle(hb)))./diff(wb);

Design a fifth-order Chebyshev Type I filter with the same edge frequency and 3 dB of passband ripple. Compute its frequency response.

[z1,p1,k1] = cheby1(n,3,wc,"s");
[b1,a1] = zp2tf(z1,p1,k1);
[h1,w1] = freqs(b1,a1,w);
gd1 = -diff(unwrap(angle(h1)))./diff(w1);

Design a fifth-order Chebyshev Type II filter with the same edge frequency and 30 dB of stopband attenuation. Compute its frequency response.

[z2,p2,k2] = cheby2(n,30,wc,"s");
[b2,a2] = zp2tf(z2,p2,k2);
[h2,w2] = freqs(b2,a2,w);
gd2 = -diff(unwrap(angle(h2)))./diff(w2);

Design a fifth-order elliptic filter with the same edge frequency, 3 dB of passband ripple, and 30 dB of stopband attenuation. Compute its frequency response.

[ze,pe,ke] = ellip(n,3,30,wc,"s");
[be,ae] = zp2tf(ze,pe,ke);
[he,we] = freqs(be,ae,w);
gde = -diff(unwrap(angle(he)))./diff(we);

Design a fifth-order Bessel filter with the same edge frequency. Compute its frequency response.

[zf,pf,kf] = besself(n,wc);
[bf,af] = zp2tf(zf,pf,kf);
[hf,wf] = freqs(bf,af,w);
gdf = -diff(unwrap(angle(hf)))./diff(wf);

Plot the attenuation in decibels. Express the frequency in gigahertz. Compare the filters.

fGHz = [wb w1 w2 we wf]/(2e9*pi);
plot(fGHz,mag2db(abs([hb h1 h2 he hf])))
axis([0 5 -45 5])
grid on
xlabel("Frequency (GHz)")
ylabel("Attenuation (dB)")
legend(["butter" "cheby1" "cheby2" "ellip" "besself"])

Figure contains an axes object. The axes object with xlabel Frequency (GHz), ylabel Attenuation (dB) contains 5 objects of type line. These objects represent butter, cheby1, cheby2, ellip, besself.

Plot the group delay in samples. Express the frequency in gigahertz and the group delay in nanoseconds. Compare the filters.

gdns = [gdb gd1 gd2 gde gdf]*1e9;
gdns(gdns<0) = NaN;
loglog(fGHz(2:end,:),gdns)
grid on
xlabel("Frequency (GHz)")
ylabel("Group delay (ns)")
legend(["butter" "cheby1" "cheby2" "ellip" "besself"])

Figure contains an axes object. The axes object with xlabel Frequency (GHz), ylabel Group delay (ns) contains 5 objects of type line. These objects represent butter, cheby1, cheby2, ellip, besself.

The Butterworth and Chebyshev Type II filters have flat passbands and wide transition bands. The Chebyshev Type I and elliptic filters roll off faster but have passband ripple. The frequency input to the Chebyshev Type II design function sets the beginning of the stopband rather than the end of the passband. The Bessel filter has approximately constant group delay along the passband.

Highpass Butterworth Filter in Cascade

Open Live Script

Design a ninth-order highpass Butterworth filter with a cutoff frequency of 300 Hz and sampling rate of 1000 Hz. Return the coefficients of the filter system as a cascade of second-order sections.

Wn = 300/(1000/2);
[B,A] = butter(9,Wn,"high","ctf")

B = 5×3

    0.2544   -0.2544         0
    0.2544   -0.5088    0.2544
    0.2544   -0.5088    0.2544
    0.2544   -0.5088    0.2544
    0.2544   -0.5088    0.2544

A = 5×3

    1.0000    0.1584         0
    1.0000    0.3264    0.0561
    1.0000    0.3575    0.1570
    1.0000    0.4189    0.3554
    1.0000    0.5304    0.7165

Plot the magnitude response of the filter.

filterAnalyzer(B,A)

Input Arguments

collapse all

`n` — Filter order
integer scalar up to 500

Filter order, specified as an integer scalar less than or equal to 500. For bandpass and bandstop designs, n represents one-half the filter order.

Data Types: double

`Wn` — Cutoff frequency
scalar | two-element vector

Cutoff frequency, specified as a scalar or a two-element vector. The cutoff frequency is the frequency at which the magnitude response of the filter is 1 / √2.

If Wn is scalar, then butter designs a lowpass or highpass filter with cutoff frequency Wn.
If Wn is the two-element vector [w1 w2], where w1 < w2, then butter designs a bandpass or bandstop filter with lower cutoff frequency w1 and higher cutoff frequency w2.
For digital filters, the cutoff frequencies must lie between 0 and 1, where 1 corresponds to the Nyquist rate—half the sample rate or π rad/sample.
For analog filters, the cutoff frequencies must be expressed in radians per second and can take on any positive value.

Data Types: double

`ftype` — Filter type
`"low"` | `"bandpass"` | `"high"` | `"stop"`

Filter type, specified as one of the following:

"low" specifies a lowpass filter with cutoff frequency Wn. "low" is the default for scalar Wn.
"high" specifies a highpass filter with cutoff frequency Wn.
"bandpass" specifies a bandpass filter of order 2n if Wn is a two-element vector. "bandpass" is the default when Wn has two elements.
"stop" specifies a bandstop filter of order 2n if Wn is a two-element vector.

Output Arguments

collapse all

`b,a` — Transfer function coefficients
row vectors

Transfer function coefficients of the filter, returned as row vectors. Given the filter order n, the function returns b and a with r samples, where r = n+1 for lowpass and highpass filters and r = 2*n+1 for bandpass and bandstop filters.

The transfer function is expressed in terms of b = [b₁ b₂ ⋯ b_r] and a = [a₁ a₂ ⋯ a_r] as one of these:

$H (z) = \frac{b_{1} + b_{2} z^{- 1} + \dots + b_{r} z^{- (r - 1)}}{a_{1} + a_{2} z^{- 1} + \dots + a_{r} z^{- (r - 1)}}$ for digital filters.
$H (s) = \frac{b_{1} s^{r - 1} + b_{2} s^{r - 2} + \dots + b_{r}}{a_{1} s^{r - 1} + a_{2} s^{r - 2} + \dots + a_{r}}$ for analog filters.

Data Types: double

`z,p,k` — Zeros, poles, and gain
column vectors, scalar

Zeros, poles, and gain of the filter, returned as two column vectors and a scalar. Given the filter order n, the function returns z and p with r samples, where r = n for lowpass and highpass filters and r = 2*n for bandpass and bandstop filters.

The transfer function is expressed in terms of z = [z₁ z₂ ⋯ z_r], p = [p₁ p₂ ⋯ p_r], and k as one of these:

$H (z) = k \frac{(1 - z_{1} z^{- 1}) (1 - z_{2} z^{- 1}) \dots (1 - z_{r} z^{- 1})}{(1 - p_{1} z^{- 1}) (1 - p_{2} z^{- 1}) \dots (1 - p_{r} z^{- 1})}$ for digital filters.
$H (s) = k \frac{(s - z_{1}) (s - z_{2}) \dots (s - z_{r})}{(s - p_{1}) (s - p_{2}) \dots (s - p_{r})}$ for analog filters.

Data Types: double

`A,B,C,D` — State-space representation
matrices

State-space representation of the filter, returned as matrices. If r = n for lowpass and highpass designs and r = 2n for bandpass and bandstop filters, then A is r × r, B is r × 1, C is 1 × r, and D is 1 × 1.

The state-space matrices relate the state vector x, the input u, and the output y through one of these equation systems.

For digital filters:

$\begin{matrix} x (k + 1) = A x (k) + B u (k) \\ y (k) = C x (k) + D u (k) . \end{matrix}$
For analog filters:

$\begin{array}{l} \dot{x} = A x + B u \\ y = C x + D u . \end{array}$

Data Types: double

`B,A` — Cascaded transfer function (CTF) coefficients
row vector | matrix

Since R2024b

Cascaded transfer function (CTF) coefficients, returned as a row vector or matrix. B and A list the numerator and denominator coefficients of the cascaded transfer function, respectively.

The sizes for B and A are L-by-(m+1) and L-by-(n+1), respectively. The function returns the first column of A as 1, thus A(1)=1 when A is a row vector.

L represents the number of filter sections.
m represents the order of the filter numerators.
n represents the order of the filter denominators.

The butter function returns the CTF coefficients with these order specifications:

m = n = 2 for lowpass and highpass filters.
m = n = 4 for bandpass and bandstop filters.

Note

To customize the CTF coefficient computation, such as setting a different order in the CTF coefficients or customizing the gain scaling, specify to return z,p,k and then use zp2ctf to obtain B,A.

For more information about the cascaded transfer function format and coefficient matrices, see Return Digital Filters in CTF Format.

`gS` — Overall system gain
real-valued scalar

Since R2024b

Overall system gain, returned as a real-valued scalar.

If you specify to return gS, the butter function normalizes the numerator coefficients so that the first column of B is 1 and returns the overall system gain in gS.
If you do not specify to return gS, the butter function uniformly distributes the system gain across all system sections using the scaleFilterSections function.

More About

collapse all

Cascaded Transfer Functions

Partitioning an IIR digital filter into cascaded sections improves its numerical stability and reduces its susceptibility to coefficient quantization errors. The cascaded form of a transfer function H(z) in terms of the L transfer functions H₁(z), H₂(z), …, H_L(z) is

$H (z) = \prod_{l = 1}^{L} H_{l} (z) = H_{1} (z) \times H_{2} (z) \times \dots \times H_{L} (z) .$

Return Digital Filters in CTF Format

Specify B and A to return the filter coefficients. You can also specify gS to return the overall system gain of the filter. By specifying these output arguments, you can design digital filters in the CTF format for analysis, visualization, and signal filtering.

Filter Coefficients

When you specify to return the numerator and denominator coefficients in the CTF format, the L-row matrices B and A are returned as

$B = [\begin{matrix} b_{11} & b_{12} & \dots & b_{1, m + 1} \\ b_{21} & b_{22} & \dots & b_{2, m + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ b_{L 1} & b_{L 2} & \dots & b_{L, m + 1} \end{matrix}], A = [\begin{matrix} 1 & a_{12} & \dots & a_{1, n + 1} \\ 1 & a_{22} & \dots & a_{2, n + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & a_{L 2} & \dots & a_{L, n + 1} \end{matrix}],$

such that the full transfer function of the filter is

$H (z) = \frac{b_{11} + b_{12} z^{- 1} + \dots + b_{1, m + 1} z^{- m}}{1 + a_{12} z^{- 1} + \dots + a_{1, n + 1} z^{- n}} \times \frac{b_{21} + b_{22} z^{- 1} + \dots + b_{2, m + 1} z^{- m}}{1 + a_{22} z^{- 1} + \dots + a_{2, n + 1} z^{- n}} \times \dots \times \frac{b_{L 1} + b_{L 2} z^{- 1} + \dots + b_{L, m + 1} z^{- m}}{1 + a_{L 2} z^{- 1} + \dots + a_{L, n + 1} z^{- n}},$

where m ≥ 0 is the numerator order of the filter and n ≥ 0 is the denominator order.

Note

To filter signals using cascaded transfer functions, use the ctffilt function.
To analyze filters represented as cascaded transfer functions, use the Filter Analyzer app. You can also use these Signal Processing Toolbox™ functions to visualize and analyze filters in CTF format:
- Time-Domain Responses — impzlength, impz, and stepz
- Frequency-Domain Responses — freqz, grpdelay, phasedelay, phasez, zerophase, and zplane
- Filter Exploration — filtord, islinphase, ismaxphase, isminphase, and isstable

Coefficients and Gain

You can specify to return the coefficients and overall system gain using the output argument triplet [B,A,gS]. In this case, the numerator coefficients are normalized, returning the filter coefficient matrices and gain as

$B = [\begin{matrix} 1 & β_{12} & \dots & β_{1, m + 1} \\ 1 & β_{22} & \dots & β_{2, m + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & β_{L 2} & \dots & β_{L, m + 1} \end{matrix}], A = [\begin{matrix} 1 & a_{12} & \dots & a_{1, n + 1} \\ 1 & a_{22} & \dots & a_{2, n + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & a_{L 2} & \dots & a_{L, n + 1} \end{matrix}], g_{S},$

so that the transfer function is

$H (z) = g_{S} (\frac{1 + β_{12} z^{- 1} + \dots + β_{1, m + 1} z^{- m}}{1 + a_{12} z^{- 1} + \dots + a_{1, n + 1} z^{- n}} \times \frac{1 + β_{22} z^{- 1} + \dots + β_{2, m + 1} z^{- m}}{1 + a_{22} z^{- 1} + \dots + a_{2, n + 1} z^{- n}} \times \dots \times \frac{1 + β_{L 2} z^{- 1} + \dots + β_{L, m + 1} z^{- m}}{1 + a_{L 2} z^{- 1} + \dots + a_{L, n + 1} z^{- n}}) .$

This transfer function is equivalent to the one defined in the Filter Coefficients section, where g_S = b₁₁×b₂₁×...×b_L1, and β_li = b_li/b_l1 for i = 1,2,…,m and l = 1,2,…,L.

Transfer Functions and CTF

Numerical Instability of Transfer Function Syntax

In general, use cascaded transfer functions ("ctf" syntaxes) to design IIR digital filters. If you design the filter using transfer functions (any of the [b,a] syntaxes), you might encounter numerical instabilities. These instabilities are due to round-off errors and can occur for an order n as low as 4. This example illustrates this limitation.

n = 6;
Fs = 200e6;
Wn = [0.5e6 6e6]/(Fs/2);
ftype = "bandpass";

% Transfer Function (TF) design
[b,a] = butter(n,Wn,ftype);    % This is an unstable filter

% CTF design
[B,A] = butter(n,Wn,ftype,"ctf");

% Compare frequency responses
[hTF,f] = freqz(b,a,8192,Fs);
hCTF = freqz(B,A,8192,Fs);

semilogx(f/1e6,db(hTF),".-",f/1e6,db(hCTF))
grid on
legend(["TF Design" "CTF Design"])
xlabel("Frequency (MHz)")
ylabel("Magnitude (dB)")

Algorithms

Butterworth filters have a magnitude response that is maximally flat in the passband and monotonic overall. This smoothness comes at the price of decreased rolloff steepness. Elliptic and Chebyshev filters generally provide steeper rolloff for a given filter order.

butter uses a five-step algorithm:

It finds the lowpass analog prototype poles, zeros, and gain using the function buttap.
It converts the poles, zeros, and gain into state-space form.
If required, it uses a state-space transformation to convert the lowpass filter into a bandpass, highpass, or bandstop filter with the desired frequency constraints.
For digital filter design, it uses bilinear to convert the analog filter into a digital filter through a bilinear transformation with frequency prewarping. Careful frequency adjustment enables the analog filters and the digital filters to have the same frequency response magnitude at Wn or at w1 and w2.
It converts the state-space filter back to its transfer function or zero-pole-gain form, as required.

References

[1] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced before R2006a

expand all

R2024b: Design digital filters using cascaded transfer functions

The butter function supports outputs in the cascaded transfer function (CTF) format.

butter

Syntax

Description

Examples

Lowpass Butterworth Transfer Function

Bandstop Butterworth Filter

Highpass Butterworth Filter

Bandpass Butterworth Filter

Comparison of Analog IIR Lowpass Filters

Highpass Butterworth Filter in Cascade

Input Arguments

`n` — Filter order
integer scalar up to 500

`Wn` — Cutoff frequency
scalar | two-element vector

`ftype` — Filter type
`"low"` | `"bandpass"` | `"high"` | `"stop"`

Output Arguments

`b,a` — Transfer function coefficients
row vectors

`z,p,k` — Zeros, poles, and gain
column vectors, scalar

`A,B,C,D` — State-space representation
matrices

`B,A` — Cascaded transfer function (CTF) coefficients
row vector | matrix

`gS` — Overall system gain
real-valued scalar

More About

Cascaded Transfer Functions

Return Digital Filters in CTF Format

Transfer Functions and CTF

Algorithms

References

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

R2024b: Design digital filters using cascaded transfer functions

See Also

Apps

Functions

butter

Syntax

Description

Examples

Lowpass Butterworth Transfer Function

Bandstop Butterworth Filter

Highpass Butterworth Filter

Bandpass Butterworth Filter

Comparison of Analog IIR Lowpass Filters

Highpass Butterworth Filter in Cascade

Input Arguments

n — Filter order integer scalar up to 500

Wn — Cutoff frequency scalar | two-element vector

ftype — Filter type "low" | "bandpass" | "high" | "stop"

Output Arguments

b,a — Transfer function coefficients row vectors

z,p,k — Zeros, poles, and gain column vectors, scalar

A,B,C,D — State-space representation matrices

B,A — Cascaded transfer function (CTF) coefficients row vector | matrix

gS — Overall system gain real-valued scalar

More About

Cascaded Transfer Functions

Return Digital Filters in CTF Format

Transfer Functions and CTF

Algorithms

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

Version History

R2024b: Design digital filters using cascaded transfer functions

See Also

Apps

Functions

`n` — Filter order
integer scalar up to 500

`Wn` — Cutoff frequency
scalar | two-element vector

`ftype` — Filter type
`"low"` | `"bandpass"` | `"high"` | `"stop"`

`b,a` — Transfer function coefficients
row vectors

`z,p,k` — Zeros, poles, and gain
column vectors, scalar

`A,B,C,D` — State-space representation
matrices

`B,A` — Cascaded transfer function (CTF) coefficients
row vector | matrix

`gS` — Overall system gain
real-valued scalar

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.