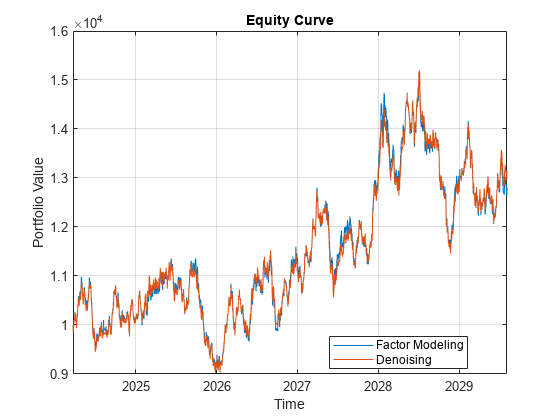投资组合优化和资产配置
量化投资管理器和风险管理器使用投资组合优化来选择投资组合中各种资产的比例。投资组合优化的目标在考虑投资组合风险的测度或间接测度的情况下最大化投资组合收益的测度或间接测度。此工具箱提供了一整套投资组合优化和分析工具,用于使用均值-方差、条件在险价值 (CVaR)、均值-绝对偏差 (MAD) 和自定义投资组合优化来执行资本配置、资产配置和风险评估。此外,工具箱还提供了一个回测框架,用于对单个周期(相对较短的时间跨度)或多个周期的投资组合配置策略和业绩归因函数进行回测。
相关主题
- 投资组合优化理论
- Portfolio Object
- Portfolio 对象工作流
- PortfolioCVaR Object
- PortfolioCVaR 对象工作流
- PortfolioMAD Object
- PortfolioMAD 对象工作流
- Using Extreme Value Theory and Copula Fitting to Generate Synthetic Data
- Black-Litterman Portfolio Optimization Using Financial Toolbox
- When to Use Portfolio Objects Over Optimization Toolbox
- Portfolio Optimization Using Factor Models
- Asset Allocation Case Study
- Risk Budgeting Portfolio
- Solve Problem for Minimum Tracking Error with Net Return Constraint
- Solve Robust Portfolio Maximum Return Problem with Ellipsoidal Uncertainty
- Hedging Using CVaR Portfolio Optimization
- 计算 CVaR 投资组合的最大收益风险比
- Backtest with Brinson Attribution to Evaluate Portfolio Performance
- Choose MINLP Solvers for Portfolio Problems
- Troubleshooting Portfolio Optimization Results
类别
- 投资组合优化理论
投资组合优化问题的背景理论
- 均值-方差投资组合优化
创建 Portfolio 对象,评估资产构成,执行均值-方差投资组合优化
- 条件在险价值投资组合优化
创建 PortfolioCVaR 对象,评估资产构成,执行 CVaR 投资组合优化
- 均值-绝对偏差投资组合优化
创建 PortfolioMAD 对象、评估资产构成、执行 MAD 投资组合优化
- 自定义投资组合优化
估计最优投资组合,指定用户定义的目标函数,定义约束
- 投资组合分析
分析投资组合的收益率方差和协方差,模拟资产的相关性,计算投资组合的在险价值 (VaR)
- 回测框架
定义投资策略,运行回测,分析策略业绩
- 业绩归因
使用 Brinson 模型计算和分析业绩归因
精选示例
使用 Financial Toolbox 的投资组合优化示例
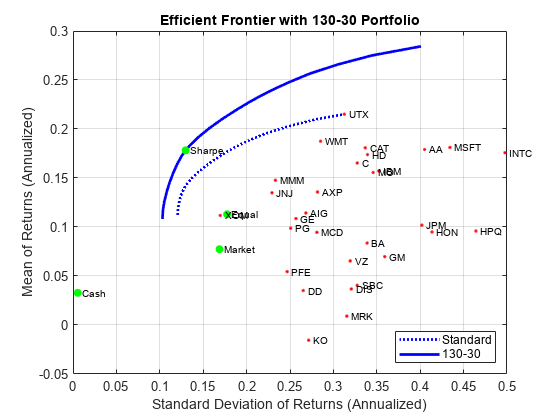
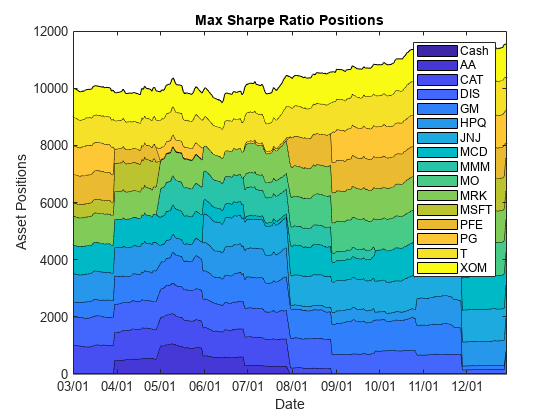
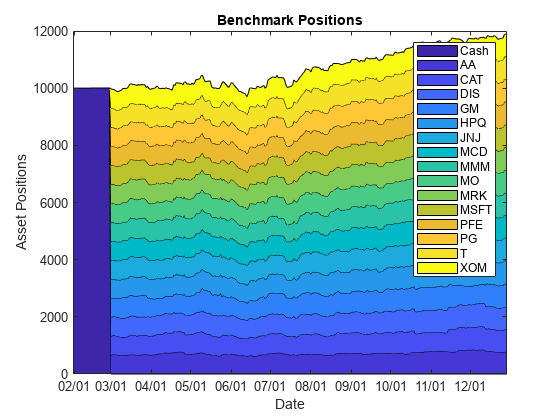
通过一组示例来了解 Portfolio 对象的主要功能。具体来说,这些示例使用 Portfolio 对象来展示如何设置重点关注两基金分离定理、交易成本和换手率约束影响的均值-方差投资组合优化问题,如何获取最大化夏普比率的投资组合,以及如何建立两种流行的对冲基金策略(美元中性和 130/30 投资组合)。
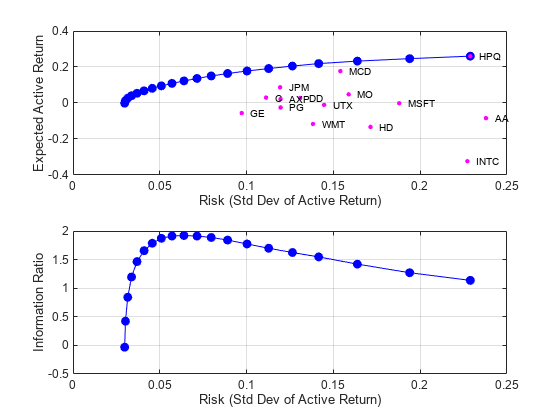
Portfolio Optimization Against a Benchmark
Demonstrates optimizing a portfolio to maximize the information ratio relative to a market benchmark.
Backtest Investment Strategies Using Financial Toolbox
Perform backtesting of portfolio strategies using a backtesting framework. Backtesting is a useful tool to compare how investment strategies perform over historical or simulated market data. This example develops five different investment strategies and then compares their performance after running over a one-year period of historical stock data. The backtesting framework is implemented in two Financial Toolbox™ classes: backtestStrategy and backtestEngine.
Backtest Investment Strategies with Trading Signals
Perform backtesting of portfolio strategies that incorporate investment signals in their trading strategy. The term signals includes any information that a strategy author needs to make with respect to trading decisions outside of the price history of the assets. Such information can include technical indicators, the outputs of machine learning models, sentiment data, macroeconomic data, and so on. This example uses three simple investment strategies based on derivative signal data:
Backtest Strategies Using Deep Learning
Construct trading strategies using a deep learning model and then backtest the strategies using the Financial Toolbox™ backtesting framework. The example uses Deep Learning Toolbox™ to train a predictive model from a set of time series and demonstrates the steps necessary to convert the model output into trading signals. It builds a variety of trading strategies that backtest the signal data over a 5-year period.
Backtest Deep Learning Model for Algorithmic Trading of Limit Order Book Data
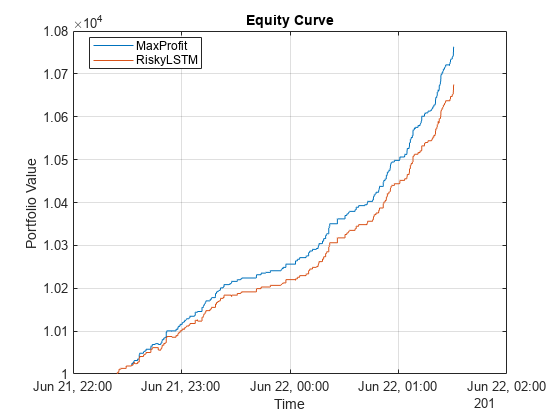
Apply a backtest strategy to measure the performance of a long short-term memory (LSTM) neural network, which is trained and validated on limit order book (LOB) data of a security.
Portfolio Optimization Using Social Performance Measure
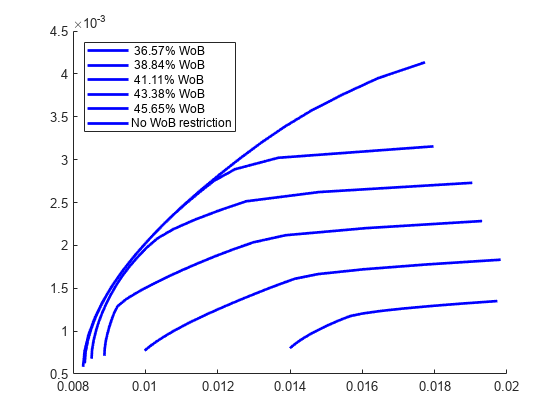
Use a Portfolio object to minimize the variance, maximize return, and maximize the average percentage of women on a company's board. The same workflow can be applied with other Environmental, Social and Governance (ESG) criteria, such as an ESG score, a climate, or a temperature score.
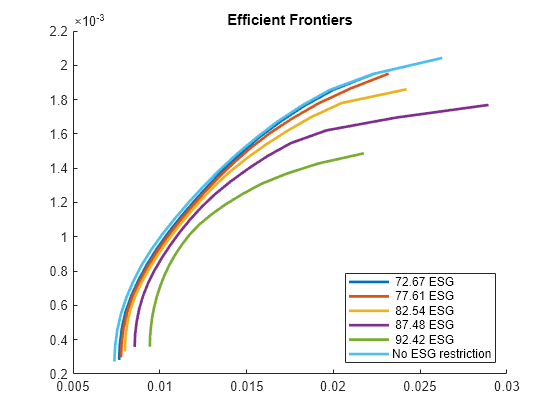
Diversify ESG Portfolios
Include qualitative factors for environmental, social, and corporate governance (ESG) in the portfolio selection process. The example extends the traditional mean-variance portfolio using a Portfolio object to include the ESG metric. First, the estimateFrontier function computes the mean-variance efficient frontier for different ESG levels. Then, the example illustrates how to combine the ESG performance measure with portfolio diversification techniques. Specifically, it introduces hybrid models that use the Herfindahl-Hirshman (HH) index and the most diversified portfolio (MDP) approach using the estimateCustomObjectivePortfolio function. Finally, the backtestEngine framework compares the returns and behavior of the different ESG strategies.
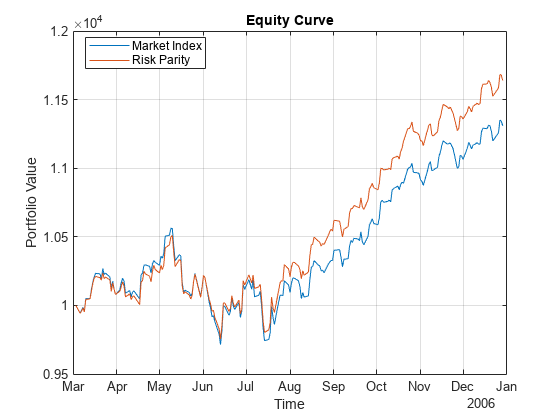
Backtest Using Risk-Based Equity Indexation
Use backtesting with a risk parity or equal risk contribution strategy rebalanced approximately every month as a risk-based indexation. In this example, you use the backtesting engine (backtestEngine) to create the risk parity strategy, that all assets in the portfolio contribute equally to the risk of the portfolio at each rebalancing period.
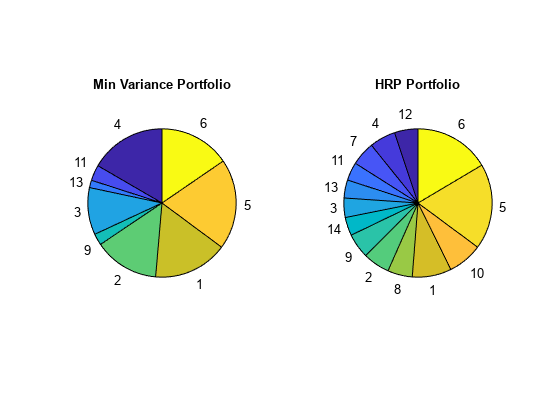
Create Hierarchical Risk Parity Portfolio
Compute a hierarchical risk parity (HRP) portfolio. You can use HRP as a technique for portfolio diversification where the assets are divided and weighted according to a hierarchical tree structure. The weights of the assets within a cluster and between clusters can be assigned in many ways. A few ideas of the ways to allocate the weights are:
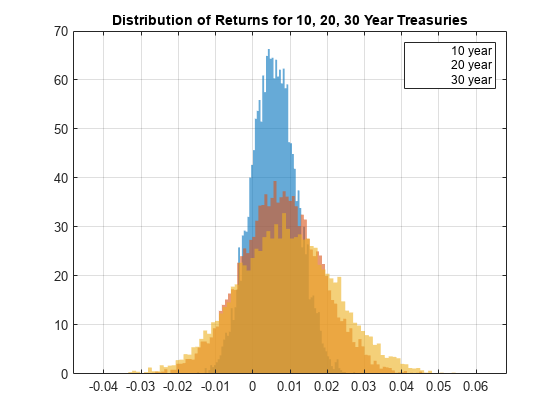
Bond Portfolio Optimization Using Portfolio Object
Use a Portfolio object to construct an optimal portfolio of 10, 20, and 30 year treasuries that will be held for a period of one month. The workflow for the overall asset allocation process is:
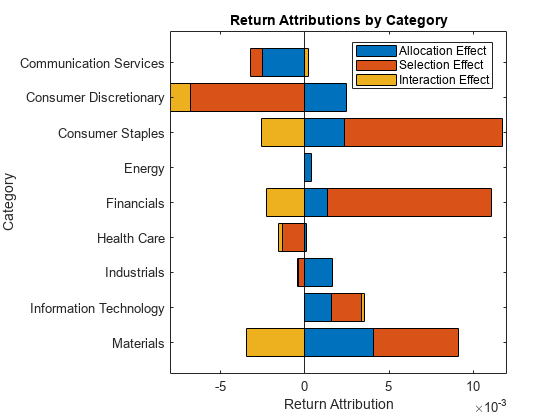
Analyze Performance Attribution Using Brinson Model
Prepare data, create a brinsonAttribution object, and then analyze the performance attribution with respect to category (sector) weights and returns. In this example, you use the categoryAttribution, categoryReturns, categoryWeights, totalAttribution, and summary functions for the analysis. Also, you can generate plots for the results, using categoryReturnsChart, categoryWeightsChart, and attributionsChart.
Diversify Portfolios Using Custom Objective
Three techniques of asset diversification in a portfolio using the estimateCustomObjectivePortfolio function with a Portfolio object. The purpose of asset diversification is to balance the exposure of the portfolio to any given asset to reduce volatility over a period of time. Given the sensitivity of the minimum variance portfolio to the estimation of the covariance matrix, some practitioners have added diversification techniques to the portfolio selection with the hope of minimizing risk measures other than the variance measures such as turnover, maximum drawdown, and so on.
Solve Tracking Error Portfolio Problems
Compute a portfolio that minimizes the tracking error subject to a benchmark portfolio. This example uses estimateCustomObjectivePortfolio to solve a problem for a minimum variance Portfolio with a tracking error penalty. The example also shows how to add the tracking error as a "soft constraint" to any portfolio optimization problem. The tracking error measures the standard deviation of the divergence between a portfolio's return and that of a benchmark.
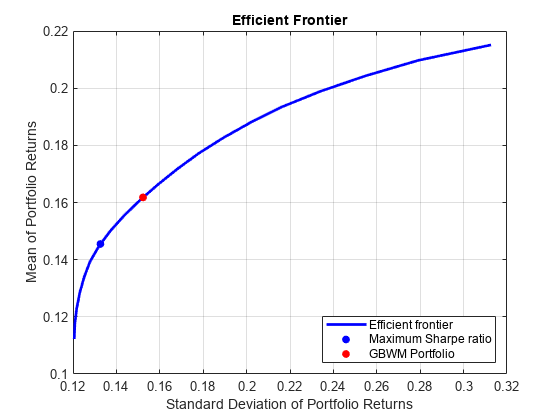
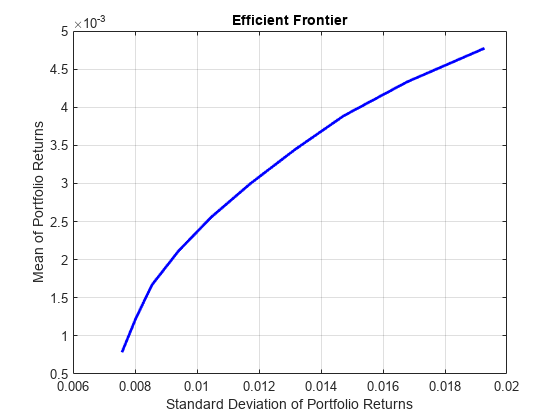
Single Period Goal-Based Wealth Management
A method for goal-based wealth management (GBWM). In GBWM, risk is not necessarily measured using the standard deviation, the value-at-risk, or any other common risk measure. Instead, risk is understood as the likelihood of not attaining an investor's goal. You choose a weight allocation that is on the traditional mean-variance efficient frontier and that also maximizes the probability of exceeding a wealth goal at the end of the investment horizon. In other words, you choose the portfolio on the efficient frontier that minimizes the risk of not attaining the investor's goal.
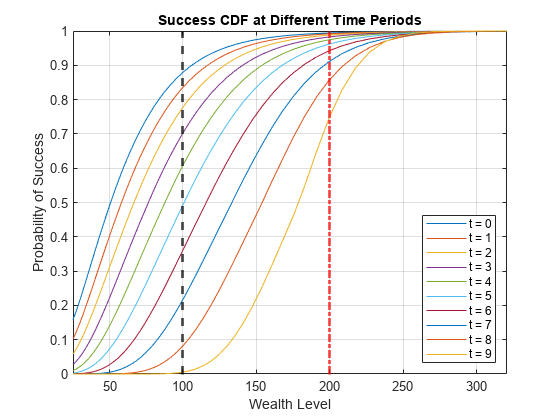
Dynamic Portfolio Allocation in Goal-Based Wealth Management for Multiple Time Periods
A dynamic programming strategy to maximize the probability of obtaining an investor's wealth goal at the end of the investment horizon. This dynamic programming strategy is known in the literature as a goal-based wealth management (GBWM) strategy. In GBWM, risk is not necessarily measured using the standard deviation, the value-at-risk, or any other common risk metric. Instead, risk is understood as the likelihood of not attaining an investor's goal. This alternative concept of risk implies that, sometimes, in order to increase the probability of attaining an investor’s goal, the optimal portfolio’s traditional risk (that is, standard deviation) must increase if the portfolio is underfunded. In other words, for the investor’s view of risk to decrease, the traditional view of risk must increase if the portfolio’s wealth is too low.
Multiperiod Goal-Based Wealth Management Using Reinforcement Learning
A reinforcement learning (RL) approach to maximize the probability of obtaining an investor's wealth goal at the end of the investment horizon. This problem is known in the literature as goal-based wealth management (GBWM). In GBWM, risk is not necessarily measured using the standard deviation, the value-at-risk, or any other common risk metric. Instead, risk is understood as the likelihood of not attaining an investor's goal. This alternative concept of risk implies that, sometimes, in order to increase the probability of attaining an investor’s goal, the optimal portfolio’s traditional risk (that is, standard deviation) must increase if the portfolio is underfunded. In other words, for the investor’s view of risk to decrease, the traditional view of risk must increase if the portfolio’s wealth is too low.
Compare Performance of Covariance Denoising with Factor Modeling Using Backtesting
Uses backtesting to compare the performance of two investment strategies that use factor information to compute the portfolio weights. The first investment strategy uses covarianceDenoising to estimate both the covariance matrix and the number of factors to use in the second investment strategy. The second investment strategy uses a principal component analysis (PCA) factor model to estimate the covariance matrix with the number of factors obtained with covarianceDenoising. The PCA factor model follows the process in Portfolio Optimization Using Factor Models.
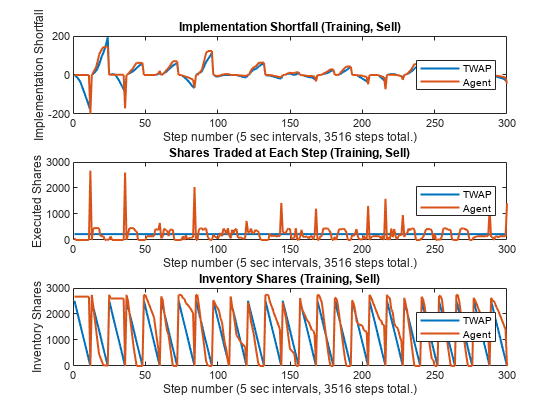
Deep Reinforcement Learning for Optimal Trade Execution
Use the Reinforcement Learning Toolbox™ and Deep Learning Toolbox™ to design agents for optimal trade execution.
混合整数均值-方差投资组合优化问题
此示例说明如何求解具有选定资产数量或条件(半连续)边界约束的均值方差投资组合优化问题。若要求解此问题,您可以使用 Portfolio 对象以及不同的混合整数非线性规划 (MINLP) 求解器。
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)