稀疏状态空间模型
在 MATLAB® 和 Simulink® 中高效地表示、组合和分析具有稀疏数据的大型状态空间模型。使用稀疏表示是理想和高效的做法,因为大型模型的稠密模型表示不仅计算成本相当高,还可能导致执行时间非常长。有关详细信息,请参阅稀疏矩阵的计算优点。
借助可用的功能,您可以:
使用稀疏模型执行时域和频域响应分析
指定稀疏模型之间以及与其他 LTI 模型的基于信号的连接
指定稀疏模型组件之间的物理耦合
在连续时间和离散时间表示之间变换稀疏模型
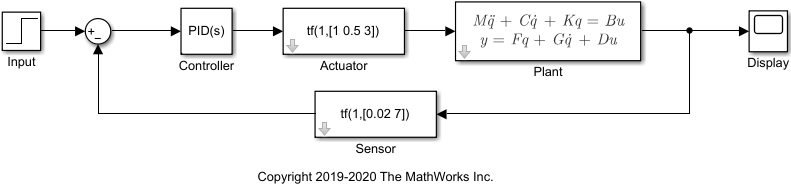
当您的 Simulink 模型具有 Descriptor State-Space (Simulink) 或 Sparse Second Order 模块时,使用
linearize(Simulink Control Design) 函数将其线性化为稀疏模型使用
linearize(Partial Differential Equation Toolbox) 函数将结构性或热 PDE 模型线性化为稀疏模型
有关稀疏模型和可用功能的更多详细信息,请参阅Sparse Model Basics。
函数
模块
| Descriptor State-Space | 模型线性隐式系统 |
| Sparse Second Order | Represent sparse second-order models in Simulink |
主题
- Sparse Model Basics
Sparse models represent state-space systems composed of large sparse matrices.
- Rigid Assembly of Model Components
Specify rigid physical couplings in a structural model.
- Thermal Modeling and Control Design for CPU Chip Cooling System
Create a CPU and heat sink thermal model, perform model order reduction, and design a controller for a cooling system.